[mathjax]
An agent which is larger than its environment can:
- Hold an exact model of the environment in its head.
- Think through the consequences of every potential course of action.
- If it doesn’t know the environment perfectly, hold every possible way the environment could be in its head, as is the case with Bayesian uncertainty.
All of these are typical of notions of rational agency.
An embedded agent can’t do any of those things, at least not in any straightforward way.

One difficulty is that, since the agent is part of the environment, modeling the environment in every detail would require the agent to model itself in every detail, which would require the agent’s self-model to be as “big” as the whole agent. An agent can’t fit inside its own head.
The lack of a crisp agent/environment boundary forces us to grapple with paradoxes of self-reference. As if representing the rest of the world weren’t already hard enough.
Embedded World-Models have to represent the world in a way more appropriate for embedded agents. Problems in this cluster include:
- the “realizability” / “grain of truth” problem: the real world isn’t in the agent’s hypothesis space
- logical uncertainty
- high-level models
- multi-level models
- ontological crises
- naturalized induction, the problem that the agent must incorporate its model of itself into its world-model
- anthropic reasoning, the problem of reasoning with how many copies of yourself exist
In a Bayesian setting, where an agent’s uncertainty is quantified by a probability distribution over possible worlds, a common assumption is “realizability”: the true underlying environment which is generating the observations is assumed to have at least some probability in the prior.
In game theory, this same property is described by saying a prior has a “grain of truth”. It should be noted, though, that there are additional barriers to getting this property in a game-theoretic setting; so, in their common usage cases, “grain of truth” is technically demanding while “realizability” is a technical convenience.
Realizability is not totally necessary in order for Bayesian reasoning to make sense. If you think of a set of hypotheses as “experts”, and the current posterior probability as how much you “trust” each expert, then learning according to Bayes’ Law, \(P(h|e) = \frac{P(e|h) \cdot P(h)}{P(e)}\), ensures a relative bounded loss property.
Specifically, if you use a prior \(\pi\), the amount worse you are in comparison to each expert \(h\) is at most \(\log \pi(h)\), since you assign at least probability \(\pi(h) \cdot h(e)\) to seeing a sequence of evidence \(e\). Intuitively, \(\pi(h)\) is your initial trust in expert \(h\), and in each case where it is even a little bit more correct than you, you increase your trust accordingly. The way you do this ensures you assign an expert probability 1 and hence copy it precisely before you lose more than \(\log \pi(h)\) compared to it.
The prior AIXI is based on is the Solomonoff prior. It is defined as the output of a universal Turing machine (UTM) whose inputs are coin-flips.
In other words, feed a UTM a random program. Normally, you’d think of a UTM as only being able to simulate deterministic machines. Here, however, the initial inputs can instruct the UTM to use the rest of the infinite input tape as a source of randomness to simulate a stochastic Turing machine.
Combining this with the previous idea about viewing Bayesian learning as a way of allocating “trust” to “experts” which meets a bounded loss condition, we can see the Solomonoff prior as a kind of ideal machine learning algorithm which can learn to act like any algorithm you might come up with, no matter how clever.
For this reason, we shouldn’t necessarily think of AIXI as “assuming the world is computable”, even though it reasons via a prior over computations. It’s getting bounded loss on its predictive accuracy as compared with any computable predictor. We should rather say that AIXI assumes all possible algorithms are computable, not that the world is.
However, lacking realizability can cause trouble if you are looking for anything more than bounded-loss predictive accuracy:
- the posterior can oscillate forever;
- probabilities may not be calibrated;
- estimates of statistics such as the mean may be arbitrarily bad;
- estimates of latent variables may be bad;
- and the identification of causal structure may not work.
So does AIXI perform well without a realizability assumption? We don’t know. Despite getting bounded loss for predictions without realizability, existing optimality results for its actions require an added realizability assumption.
First, if the environment really is sampled from the Solomonoff distribution, AIXI gets the maximum expected reward. But this is fairly trivial; it is essentially the definition of AIXI.
Second, if we modify AIXI to take somewhat randomized actions—Thompson sampling—there is an asymptotic optimality result for environments which act like any stochastic Turing machine.
So, either way, realizability was assumed in order to prove anything. (See Jan Leike, Nonparametric General Reinforcement Learning.)
But the concern I’m pointing at is not “the world might be uncomputable, so we don’t know if AIXI will do well”; this is more of an illustrative case. The concern is that AIXI is only able to define intelligence or rationality by constructing an agent much, much bigger than the environment which it has to learn about and act within.
Laurent Orseau provides a way of thinking about this in “Space-Time Embedded Intelligence”. However, his approach defines the intelligence of an agent in terms of a sort of super-intelligent designer who thinks about reality from outside, selecting an agent to place into the environment.
Embedded agents don’t have the luxury of stepping outside of the universe to think about how to think. What we would like would be a theory of rational belief for situated agents which provides foundations that are similarly as strong as the foundations Bayesianism provides for dualistic agents.
Imagine a computer science theory person who is having a disagreement with a programmer. The theory person is making use of an abstract model. The programmer is complaining that the abstract model isn’t something you would ever run, because it is computationally intractable. The theory person responds that the point isn’t to ever run it. Rather, the point is to understand some phenomenon which will also be relevant to more tractable things which you would want to run.
I bring this up in order to emphasize that my perspective is a lot more like the theory person’s. I’m not talking about AIXI to say “AIXI is an idealization you can’t run”. The answers to the puzzles I’m pointing at don’t need to run. I just want to understand some phenomena.
However, sometimes a thing that makes some theoretical models less tractable also makes that model too different from the phenomenon we’re interested in.
The way AIXI wins games is by assuming we can do true Bayesian updating over a hypothesis space, assuming the world is in our hypothesis space, etc. So it can tell us something about the aspect of realistic agency that’s approximately doing Bayesian updating over an approximately-good-enough hypothesis space. But embedded agents don’t just need approximate solutions to that problem; they need to solve several problems that are different in kind from that problem.
One major obstacle a theory of embedded agency must deal with is self-reference.
Paradoxes of self-reference such as the liar paradox make it not just wildly impractical, but in a certain sense impossible for an agent’s world-model to accurately reflect the world.
The liar paradox concerns the status of the sentence “This sentence is not true”. If it were true, it must be false; and if not true, it must be true.
The difficulty comes in part from trying to draw a map of a territory which includes the map itself.
This is fine if the world “holds still” for us; but because the map is in the world, different maps create different worlds.
Suppose our goal is to make an accurate map of the final route of a road which is currently under construction. Suppose we also know that the construction team will get to see our map, and that construction will proceed so as to disprove whatever map we make. This puts us in a liar-paradox-like situation.

Problems of this kind become relevant for decision-making in the theory of games. A simple game of rock-paper-scissors can introduce a liar paradox if the players try to win, and can predict each other better than chance.
Game theory solves this type of problem with game-theoretic equilibria. But the problem ends up coming back in a different way.
I mentioned that the problem of realizability takes on a different character in the context of game theory. In an ML setting, realizability is a potentially unrealistic assumption, but can usually be assumed consistently nonetheless.
In game theory, on the other hand, the assumption itself may be inconsistent. This is because games commonly yield paradoxes of self-reference.
Because there are so many agents, it is no longer possible in game theory to conveniently make an “agent” a thing which is larger than a world. So game theorists are forced to investigate notions of rational agency which can handle a large world.
Unfortunately, this is done by splitting up the world into “agent” parts and “non-agent” parts, and handling the agents in a special way. This is almost as bad as dualistic models of agency.
In rock-paper-scissors, the liar paradox is resolved by stipulating that each player play each move with \(1/3\) probability. If one player plays this way, then the other loses nothing by doing so. This way of introducing probabilistic play to resolve would-be paradoxes of game theory is called a Nash equilibrium.
We can use Nash equilibria to prevent the assumption that the agents correctly understand the world they’re in from being inconsistent. However, that works just by telling the agents what the world looks like. What if we want to model agents who learn about the world, more like AIXI?
The grain of truth problem is the problem of formulating a reasonably bound prior probability distribution which would allow agents playing games to place some positive probability on each other’s true (probabilistic) behavior, without knowing it precisely from the start.
Until recently, known solutions to the problem were quite limited. Benja Fallenstein, Jessica Taylor, and Paul Christiano’s “Reflective Oracles: A Foundation for Classical Game Theory” provides a very general solution. For details, see “A Formal Solution to the Grain of Truth Problem” by Jan Leike, Jessica Taylor, and Benja Fallenstein.
You might think that stochastic Turing machines can represent Nash equilibria just fine.

But if you’re trying to produce Nash equilibria as a result of reasoning about other agents, you’ll run into trouble. If each agent models the other’s computation and tries to run it to see what the other agent does, you’ve just got an infinite loop.
There are some questions Turing machines just can’t answer—in particular, questions about the behavior of Turing machines. The halting problem is the classic example.
Turing studied “oracle machines” to examine what would happen if we could answer such questions. An oracle is like a book containing some answers to questions which we were unable to answer before.
But ordinarily, we get a hierarchy. Type B machines can answer questions about whether type A machines halt, type C machines have the answers about types A and B, and so on, but no machines have answers about their own type.
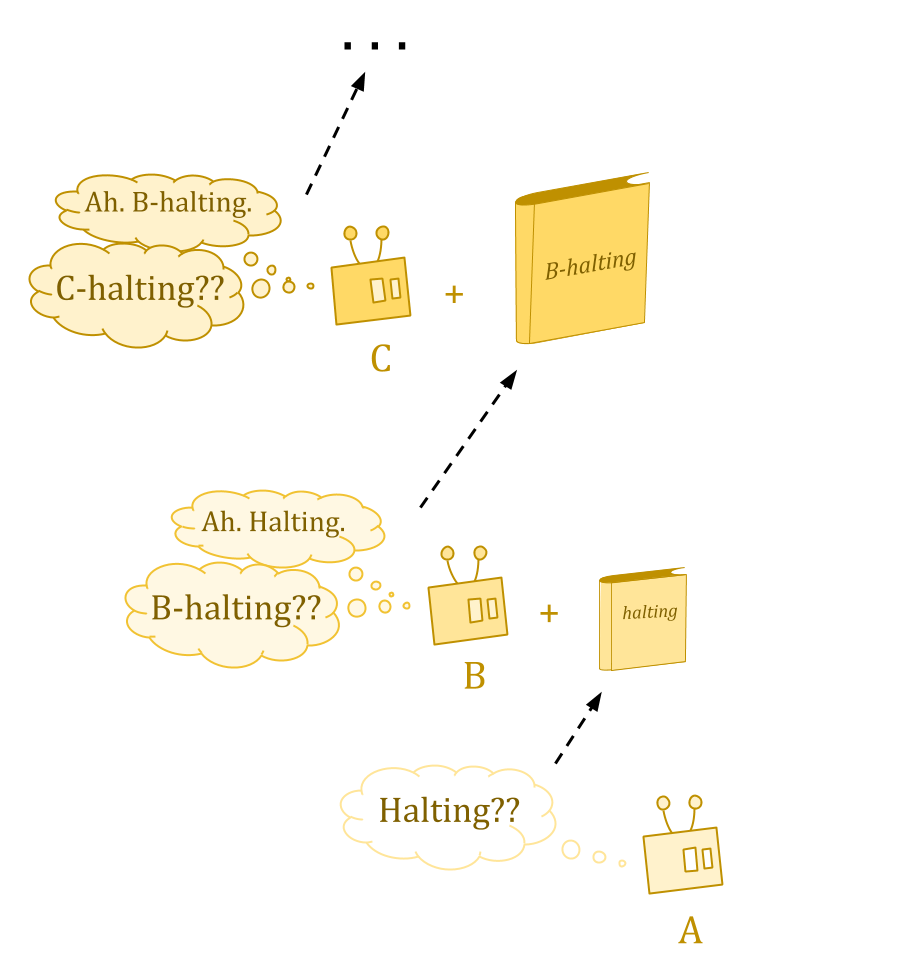
Reflective oracles work by twisting the ordinary Turing universe back on itself, so that rather than an infinite hierarchy of ever-stronger oracles, you define an oracle that serves as its own oracle machine.

This would normally introduce contradictions, but reflective oracles avoid this by randomizing their output in cases where they would run into paradoxes. So reflective oracle machines are stochastic, but they’re more powerful than regular stochastic Turing machines.
That’s how reflective oracles address the problems we mentioned earlier of a map that’s itself part of the territory: randomize.
Reflective oracles also solve the problem with game-theoretic notions of rationality I mentioned earlier. It allows agents to be reasoned about in the same manner as other parts of the environment, rather than treating them as a fundamentally special case. They’re all just computations-with-oracle-access.
However, models of rational agents based on reflective oracles still have several major limitations. One of these is that agents are required to have unlimited processing power, just like AIXI, and so are assumed to know all of the consequences of their own beliefs.
In fact, knowing all the consequences of your beliefs—a property known as logical omniscience—turns out to be rather core to classical Bayesian rationality.
So far, I’ve been talking in a fairly naive way about the agent having beliefs about hypotheses, and the real world being or not being in the hypothesis space.
It isn’t really clear what any of that means.
Depending on how we define things, it may actually be quite possible for an agent to be smaller than the world and yet contain the right world-model—it might know the true physics and initial conditions, but only be capable of inferring their consequences very approximately.
Humans are certainly used to living with shorthands and approximations. But realistic as this scenario may be, it is not in line with what it usually means for a Bayesian to know something. A Bayesian knows the consequences of all of its beliefs.
Uncertainty about the consequences of your beliefs is logical uncertainty. In this case, the agent might be empirically certain of a unique mathematical description pinpointing which universe she’s in, while being logically uncertain of most consequences of that description.
Modeling logical uncertainty requires us to have a combined theory of logic (reasoning about implications) and probability (degrees of belief).
Logic and probability theory are two great triumphs in the codification of rational thought. Logic provides the best tools for thinking about self-reference, while probability provides the best tools for thinking about decision-making. However, the two don’t work together as well as one might think.
They may seem superficially compatible, since probability theory is an extension of Boolean logic. However, Gödel’s first incompleteness theorem shows that any sufficiently rich logical system is incomplete: not only does it fail to decide every sentence as true or false, but it also has no computable extension which manages to do so.
(See the post “An Untrollable Mathematician Illustrated” for more illustration of how this messes with probability theory.)
This also applies to probability distributions: no computable distribution can assign probabilities in a way that’s consistent with a sufficiently rich theory. This forces us to choose between using an uncomputable distribution, or using a distribution which is inconsistent.
Sounds like an easy choice, right? The inconsistent theory is at least computable, and we are after all trying to develop a theory of logical non-omniscience. We can just continue to update on facts which we prove, bringing us closer and closer to consistency.
Unfortunately, this doesn’t work out so well, for reasons which connect back to realizability. Remember that there are no computable probability distributions consistent with all consequences of sound theories. So our non-omniscient prior doesn’t even contain a single correct hypothesis.
This causes pathological behavior as we condition on more and more true mathematical beliefs. Beliefs wildly oscillate rather than approaching reasonable estimates.
Taking a Bayesian prior on mathematics, and updating on whatever we prove, does not seem to capture mathematical intuition and heuristic conjecture very well—unless we restrict the domain and craft a sensible prior.
Probability is like a scale, with worlds as weights. An observation eliminates some of the possible worlds, removing weights and shifting the balance of beliefs.
Logic is like a tree, growing from the seed of axioms according to inference rules. For real-world agents, the process of growth is never complete; you never know all the consequences of each belief.
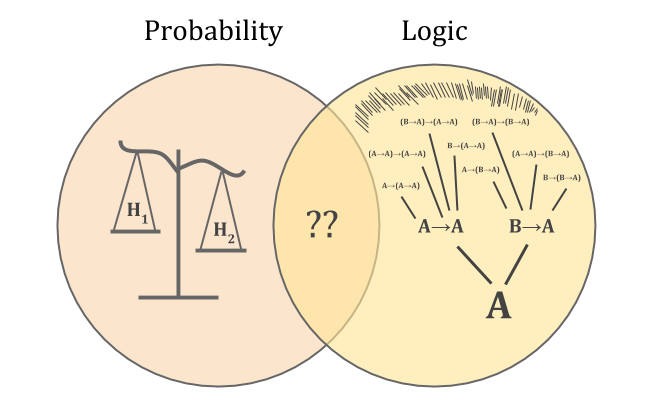
Without knowing how to combine the two, we can’t characterize reasoning probabilistically about math. But the “scale versus tree” problem also means that we don’t know how ordinary empirical reasoning works.
Bayesian hypothesis testing requires each hypothesis to clearly declare which probabilities it assigns to which observations. That way, you know how much to rescale the odds when you make an observation. If we don’t know the consequences of a belief, we don’t know how much credit to give it for making predictions.
This is like not knowing where to place the weights on the scales of probability. We could try putting weights on both sides until a proof rules one out, but then the beliefs just oscillate forever rather than doing anything useful.
This forces us to grapple directly with the problem of a world that’s larger than the agent. We want some notion of boundedly rational beliefs about uncertain consequences; but any computable beliefs about logic must have left out something, since the tree of logical implications will grow larger than any container.
For a Bayesian, the scales of probability are balanced in precisely such a way that no Dutch book can be made against them—no sequence of bets that are a sure loss. But you can only account for all Dutch books if you know all the consequences of your beliefs. Absent that, someone who has explored other parts of the tree can Dutch-book you.
But human mathematicians don’t seem to run into any special difficulty in reasoning about mathematical uncertainty, any more than we do with empirical uncertainty. So what characterizes good reasoning under mathematical uncertainty, if not immunity to making bad bets?
One answer is to weaken the notion of Dutch books so that we only allow bets based on quickly computable parts of the tree. This is one of the ideas behind Garrabrant et al.’s “Logical Induction”, an early attempt at defining something like “Solomonoff induction, but for reasoning that incorporates mathematical uncertainty”.
Another consequence of the fact that the world is bigger than you is that you need to be able to use high-level world models: models which involve things like tables and chairs.
This is related to the classical symbol grounding problem; but since we want a formal analysis which increases our trust in some system, the kind of model which interests us is somewhat different. This also relates to transparency and informed oversight: world-models should be made out of understandable parts.
A related question is how high-level reasoning and low-level reasoning relate to each other and to intermediate levels: multi-level world models.
Standard probabilistic reasoning doesn’t provide a very good account of this sort of thing. It’s as though you have different Bayes nets which describe the world at different levels of accuracy, and processing power limitations force you to mostly use the less accurate ones, so you have to decide how to jump to the more accurate as needed.
Additionally, the models at different levels don’t line up perfectly, so you have a problem of translating between them; and the models may have serious contradictions between them. This might be fine, since high-level models are understood to be approximations anyway, or it could signal a serious problem in the higher- or lower-level models, requiring their revision.
This is especially interesting in the case of ontological crises, in which objects we value turn out not to be a part of “better” models of the world.
It seems fair to say that everything humans value exists in high-level models only, which from a reductionistic perspective is “less real” than atoms and quarks. However, because our values aren’t defined on the low level, we are able to keep our values even when our knowledge of the low level radically shifts. (We would also like to be able to say something about what happens to values if the high level radically shifts.)
Another critical aspect of embedded world models is that the agent itself must be in the model, since the agent seeks to understand the world, and the world cannot be fully separated from oneself. This opens the door to difficult problems of self-reference and anthropic decision theory.
Naturalized induction is the problem of learning world-models which include yourself in the environment. This is challenging because (as Caspar Oesterheld has put it) there is a type mismatch between “mental stuff” and “physics stuff”.
AIXI conceives of the environment as if it were made with a slot which the agent fits into. We might intuitively reason in this way, but we can also understand a physical perspective from which this looks like a bad model. We might imagine instead that the agent separately represents: self-knowledge available to introspection; hypotheses about what the universe is like; and a “bridging hypothesis” connecting the two.
There are interesting questions of how this could work. There’s also the question of whether this is the right structure at all. It’s certainly not how I imagine babies learning.
Thomas Nagel would say that this way of approaching the problem involves “views from nowhere”; each hypothesis posits a world as if seen from outside. This is perhaps a strange thing to do.
A special case of agents needing to reason about themselves is agents needing to reason about their future self.
To make long-term plans, agents need to be able to model how they’ll act in the future, and have a certain kind of trust in their future goals and reasoning abilities. This includes trusting future selves that have learned and grown a great deal.
In a traditional Bayesian framework, “learning” means Bayesian updating. But as we noted, Bayesian updating requires that the agent start out large enough to consider a bunch of ways the world can be, and learn by ruling some of these out.
Embedded agents need resource-limited, logically uncertain updates, which don’t work like this.
Unfortunately, Bayesian updating is the main way we know how to think about an agent progressing through time as one unified agent. The Dutch book justification for Bayesian reasoning is basically saying this kind of updating is the only way to not have the agent’s actions on Monday work at cross purposes, at least a little, to the agent’s actions on Tuesday.
Embedded agents are non-Bayesian. And non-Bayesian agents tend to get into wars with their future selves.
Which brings us to our next set of problems: robust delegation.
This is part of Abram Demski and Scott Garrabrant’s Embedded Agency sequence. Next part: Robust Delegation.