 Nate Soares’ recent decision theory paper with Ben Levinstein, “Cheating Death in Damascus,” prompted some valuable questions and comments from an acquaintance (anonymized here). I’ve put together edited excerpts from the commenter’s email below, with Nate’s responses.
Nate Soares’ recent decision theory paper with Ben Levinstein, “Cheating Death in Damascus,” prompted some valuable questions and comments from an acquaintance (anonymized here). I’ve put together edited excerpts from the commenter’s email below, with Nate’s responses.
The discussion concerns functional decision theory (FDT), a newly proposed alternative to causal decision theory (CDT) and evidential decision theory (EDT). Where EDT says “choose the most auspicious action” and CDT says “choose the action that has the best effects,” FDT says “choose the output of one’s decision algorithm that has the best effects across all instances of that algorithm.”
FDT usually behaves similarly to CDT. In a one-shot prisoner’s dilemma between two agents who know they are following FDT, however, FDT parts ways with CDT and prescribes cooperation, on the grounds that each agent runs the same decision-making procedure, and that therefore each agent is effectively choosing for both agents at once. ((CDT prescribes defection in this dilemma, on the grounds that one’s action cannot cause the other agent to cooperate. FDT outperforms CDT in Newcomblike dilemmas like these, while also outperforming EDT in other dilemmas, such as the smoking lesion problem and XOR blackmail.))
Below, Nate provides some of his own perspective on why FDT generally achieves higher utility than CDT and EDT. Some of the stances he sketches out here are stronger than the assumptions needed to justify FDT, but should shed some light on why researchers at MIRI think FDT can help resolve a number of longstanding puzzles in the foundations of rational action.
Anonymous: This is great stuff! I’m behind on reading loads of papers and books for my research, but this came across my path and hooked me, which speaks highly of how interesting is the content and the sense that this paper is making progress.
My general take is that you are right that these kinds of problems need to be specified in more detail. However, my guess is that once you do so, game theorists would get the right answer. Perhaps that’s what FDT is: it’s an approach to clarifying ambiguous games that leads to a formalism where people like Pearl and myself can use our standard approaches to get the right answer.
I know there’s a lot of inertia in the “decision theory” language, so probably it doesn’t make sense to change. But if there were no such sunk costs, I would recommend a different framing. It’s not that people’s decision theories are wrong; it’s that they are unable to correctly formalize problems in which there are high-performance predictors. You show how to do that, using the idea of intervening on (i.e., choosing between putative outputs of) the algorithm, rather than intervening on actions. Everything else follows from a sufficiently precise and non-contradictory statement of the decision problem.
Probably the easiest move this line of work could make to ease this knee-jerk response of mine in defense of mainstream Bayesian game theory is to just be clear that CDT is not meant to capture mainstream Bayesian game theory. Rather, it is a model of one response to a class of problems not normally considered and for which existing approaches are ambiguous.
Nate Soares: I don’t take this view myself. My view is more like: When you add accurate predictors to the Rube Goldberg machine that is the universe — which can in fact be done — the future of that universe can be determined by the behavior of the algorithm being predicted. The algorithm that we put in the “thing-being-predicted” slot can do significantly better if its reasoning on the subject of which actions to output respects the universe’s downstream causal structure (which is something CDT and FDT do, but which EDT neglects), and it can do better again if its reasoning also respects the world’s global logical structure (which is done by FDT alone).
We don’t know exactly how to respect this wider class of dependencies in general yet, but we do know how to do it in many simple cases. While it agrees with modern decision theory and game theory in many simple situations, its prescriptions do seem to differ in non-trivial applications.
The main case where we can easily see that FDT is not just a better tool for formalizing game theorists’ traditional intuitions is in prisoner’s dilemmas. Game theory is pretty adamant about the fact that it’s rational to defect in a one-shot PD, whereas two FDT agents facing off in a one-shot PD will cooperate.
In particular, classical game theory employs a “common knowledge of shared rationality” assumption which, when you look closely at it, cashes out more or less as “common knowledge that all parties are using CDT and this axiom.” Game theory where common knowledge of shared rationality is defined to mean “common knowledge that all parties are using FDT and this axiom” gives substantially different results, such as cooperation in one-shot PDs.
Anonymous: When I’ve read MIRI work on CDT in the past, it seemed to me to describe what standard game theorists mean by rationality. But at least in cases like Murder Lesion, I don’t think it’s fair to say that standard game theorists would prescribe CDT. It might be better to say that standard game theory doesn’t consider these kinds of settings, and there are multiple ways of responding to them, CDT being one.
But I also suspect that many of these perfect prediction problems are internally inconsistent, and so it’s irrelevant what CDT would prescribe, since the problem cannot arise. That is, it’s not reasonable to say game theorists would recommend such-and-such in a certain problem, when the problem postulates that the actor always has incorrect expectations; “all agents have correct expectations” is a core property of most game-theoretic problems.
The Death in Damascus problem for CDT agents is a good example of this. In this problem, either Death will not find the CDT agent with certainty, or the CDT agent will never have correct beliefs about her own actions, or she will be unable to best respond to her own beliefs.
So the problem statement (“Death finds the agent with certainty”) rules out typical assumptions of a rational actor: that it has rational expectations (including about its own behavior), and that it can choose the preferred action in response to its beliefs. The agent can only have correct beliefs if she believes that she has such-and-such belief about which city she’ll end up in, but doesn’t select the action that is the best response to that belief.
Nate: I contest that last claim. The trouble is in the phrase “best response”, where you’re using CDT’s notion of what counts as the best response. According to FDT’s notion of “best response”, the best response to your beliefs in the Death in Damascus problem is to stay in Damascus, if we’re assuming it costs nonzero utility to make the trek to Aleppo.
In order to define what the best response to a problem is, we normally invoke a notion of counterfactuals — what are your available responses, and what do you think follows from them? But the question of how to set up those counterfactuals is the very point under contention.
So I’ll grant that if you define “best response” in terms of CDT’s counterfactuals, then Death in Damascus rules out the typical assumptions of a rational actor. If you use FDT’s counterfactuals (i.e., counterfactuals that respect the full range of subjunctive dependencies), however, then you get to keep all the usual assumptions of rational actors. We can say that FDT has the pre-theoretic advantage over CDT that it allows agents to exhibit sensible-seeming properties like these in a wider array of problems.
Anonymous: The presentation of the Death in Damascus problem for CDT feels weird to me. CDT might also just turn up an error, since one of its assumptions is violated by the problem. Or it might cycle through beliefs forever… The expected utility calculation here seems to give some credence to the possibility of dodging death, which is assumed to be impossible, so it doesn’t seem to me to correctly reason in a CDT way about where death will be.
For some reason I want to defend the CDT agent, and say that it’s not fair to say they wouldn’t realize that their strategy produces a contradiction (given the assumptions of rational belief and agency) in this problem.
Nate: There are a few different things to note here. First is that my inclination is always to evaluate CDT as an algorithm: if you built a machine that follows the CDT equation to the very letter, what would it do?
The answer here, as you’ve rightly noted above, is that the CDT equation isn’t necessarily defined when the input is a problem like Death in Damascus, and I agree that simple definitions of CDT yield algorithms that would either enter an infinite loop or crash. The third alternative is that the agent notices the difficulty and engages in some sort of reflective-equilibrium-finding procedure; variants of CDT with this sort of patch were invented more or less independently by Joyce and Arntzenius to do exactly that. In the paper, we discuss the variants that run an equilibrium-finding procedure and show that the equilibrium is still unsatisfactory; but we probably should have been more explicit about the fact that vanilla CDT either crashes or loops.
Second, I acknowledge that there’s still a strong intuition that an agent should in some sense be able to reflect on their own instability, look at the problem statement, and say, “Aha, I see what’s going on here; Death will find me no matter what I choose; I’d better find some other way to make the decision.” However, this sort of response is explicitly ruled out by the CDT equation: CDT says you must evaluate your actions as if they were subjunctively independent of everything that doesn’t causally depend on them.
In other words, you’re correct that CDT agents know intellectually that they cannot escape Death, but the CDT equation requires agents to imagine that they can, and to act on this basis.
And, to be clear, it is not a strike against an algorithm for it to prescribe making actions by reasoning about impossible scenarios — any deterministic algorithm attempting to reason about what it “should do” must imagine some impossibilities, because a deterministic algorithm has to reason about the consequences of doing lots of different things, but is in fact only going to do one thing.
The question at hand is which impossibilities are the right ones to imagine, and the claim is that in scenarios with accurate predictors, CDT prescribes imagining the wrong impossibilities, including impossibilities where it escapes Death.
Our human intuitions say that we should reflect on the problem statement and eventually realize that escaping Death is in some sense “too impossible to consider”. But this directly contradicts the advice of CDT. Following this intuition requires us to make our beliefs obey a logical-but-not-causal constraint in the problem statement (“Death is a perfect predictor”), which FDT agents can do but CDT agents can’t. On close examination, the “shouldn’t CDT realize this is wrong?” intuition turns out to be an argument for FDT in another guise. (Indeed, pursuing this intuition is part of how FDT’s predecessors were discovered!)
Third, I’ll note it’s an important virtue in general for decision theories to be able to reason correctly in the face of apparent inconsistency. Consider the following simple example:
An agent has a choice between taking $1 or taking $100. There is an extraordinarily tiny but nonzero probability that a cosmic ray will spontaneously strike the agent’s brain in such a way that they will be caused to do the opposite of whichever action they would normally do. If they learn that they have been struck by a cosmic ray, then they will also need to visit the emergency room to ensure there’s no lasting brain damage, at a cost of $1000. Furthermore, the agent knows that they take the $100 if and only if they are hit by the cosmic ray.
When faced with this problem, EDT agents reason: “If I take the $100, then I must have been hit by the cosmic ray, which means that I lose $900 on net. I therefore prefer the $1.” They then take the $1 (except in cases where they have been hit by the cosmic ray).
Since this is just what the problem statement says — “the agent knows that they take the $100 if and only if they are hit by the cosmic ray” — the problem is perfectly consistent, as is EDT’s response to the problem. EDT only cares about correlation, not dependency; so EDT agents are perfectly happy to buy into self-fulfilling prophecies, even when it means turning their backs on large sums of money.
What happens when we try to pull this trick on a CDT agent? She says, “Like hell I only take the $100 if I’m hit by the cosmic ray!” and grabs the $100 — thus revealing your problem statement to be inconsistent if the agent runs CDT as opposed to EDT.
The claim that “the agent knows that they take the $100 if and only if they are hit by the cosmic ray” contradicts the definition of CDT, which requires that agents of CDT refuse to leave free money on the table. As you may verify, FDT also renders the problem statement inconsistent, for similar reasons. The definition of EDT, on the other hand, is fully consistent with the problem as stated.
This means that if you try to put EDT into the above situation — controlling its behavior by telling it specific facts about itself — you will succeed; whereas if you try to put CDT into the above situation, you will fail, and the supposed facts will be revealed as lies. Whether or not the above problem statement is consistent depends on the algorithm that the agent runs, and the design of the algorithm controls the degree to which you can put that algorithm in bad situations.
We can think of this as a case of FDT and CDT succeeding in making a low-utility universe impossible, where EDT fails to make a low-utility universe impossible. The whole point of implementing a decision theory on a piece of hardware and running it is to make bad futures-of-our-universe impossible (or at least very unlikely). It’s a feature of a decision theory, and not a bug, for there to be some problems where one tries to describe a low-utility state of affairs and the decision theory says, “I’m sorry, but if you run me in that problem, your problem will be revealed as inconsistent”. ((There are some fairly natural ways to cash out Murder Lesion where CDT accepts the problem and FDT forces a contradiction, but we decided not to delve into that interpretation in the paper.
Tangentially, I’ll note that one of the most common defenses of CDT similarly turns on the idea that certain dilemmas are “unfair” to CDT. Compare, for example, David Lewis’ “Why Ain’cha Rich?”
It’s obviously possible to define decision problems that are “unfair” in the sense that they just reward or punish agents for having a certain decision theory. We can imagine a dilemma where a predictor simply guesses whether you’re implementing FDT, and gives you $1,000,000 if so. Since we can construct symmetric dilemmas that instead reward CDT agents, EDT agents, etc., these dilemmas aren’t very interesting, and can’t help us choose between theories.
Dilemmas like Newcomb’s problem and Death in Damascus, however, don’t evaluate agents based on their decision theories. They evaluate agents based on their actions, and the task of the decision theory is to determine which action is best. If it’s unfair to criticize CDT for making the wrong choice in problems like this, then it’s hard to see on what grounds we can criticize any agent for making a wrong choice in any problem, since one can always claim that one is merely at the mercy of one’s decision theory.))
This doesn’t contradict anything you’ve said; I say it only to highlight how little we can conclude from noticing that an agent is reasoning about an inconsistent state of affairs. Reasoning about impossibilities is the mechanism by which decision theories produce actions that force the outcome to be desirable, so we can’t conclude that an agent has been placed in an unfair situation from the fact that the agent is forced to reason about an impossibility.
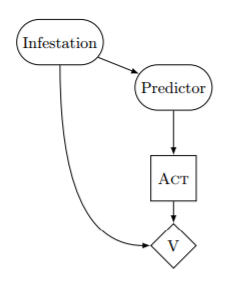
An agent has been alerted to a rumor that her house has a terrible termite infestation, which would cost her $1,000,000 in damages. She doesn’t know whether this rumor is true. A greedy and accurate predictor with a strong reputation for honesty has learned whether or not it’s true, and drafts a letter:
“I know whether or not you have termites, and I have sent you this letter iff exactly one of the following is true: (i) the rumor is false, and you are going to pay me $1,000 upon receiving this letter; or (ii) the rumor is true, and you will not pay me upon receiving this letter.”
The predictor then predicts what the agent would do upon receiving the letter, and sends the agent the letter iff exactly one of (i) or (ii) is true. Thus, the claim made by the letter is true. Assume the agent receives the letter. Should she pay up?
In this scenario, EDT pays the blackmailer, while CDT and FDT refuse to pay. See the “Cheating Death in Damascus” paper for more details.))
Anonymous: Something still seems fishy to me about decision problems that assume perfect predictors. If I’m being predicted with 100% accuracy in the XOR blackmail problem, then this means that I can induce a contradiction. If I follow FDT and CDT’s recommendation of never paying, then I only receive a letter when I have termites. But if I pay, then I must be in the world where I don’t have termites, as otherwise there is a contradiction.
So it seems that I am able to intervene on the world in a way that changes the state of termites for me now, given that I’ve received a letter. That is, the best strategy when starting is to never pay, but the best strategy given that I will receive a letter is to pay. The weirdness arises because I’m able to intervene on the algorithm, but we are conditioning on a fact of the world that depends on my algorithm.
Not sure if this confusion makes sense to you. My gut says that these kinds of problems are often self-contradicting, at least when we assert 100% predictive performance. I would prefer to work it out from the ex ante situation, with specified probabilities of getting termites, and see if it is the case that changing one’s strategy (at the algorithm level) is possible without changing the probability of termites to maintain consistency of the prediction claim.
Nate: First, I’ll note that the problem goes through fine if the prediction is only correct 99% of the time. If the difference between “cost of termites” and “cost of paying” is sufficient high, then the problem can probably go through even if the predictor is only correct 51% of the time.
That said, the point of this example is to draw attention to some of the issues you’re raising here, and I think that these issues are just easier to think about when we assume 100% predictive accuracy.
The claim I dispute is this one: “That is, the best strategy when starting is to never pay, but the best strategy given that I will receive a letter is to pay.” I claim that the best strategy given that you receive the letter is to not pay, because whether you pay has no effect on whether or not you have termites. Whenever you pay, no matter what you’ve learned, you’re basically just burning $1000.
That said, you’re completely right that these decision problems have some inconsistent branches, though I claim that this is true of any decision problem. In a deterministic universe with deterministic agents, all “possible actions” the agent “could take” save one are not going to be taken, and thus all “possibilities” save one are in fact inconsistent given a sufficiently full formal specification.
I also completely endorse the claim that this set-up allows the predicted agent to induce a contradiction. Indeed, I claim that all decision-making power comes from the ability to induce contradictions: the whole reason to write an algorithm that loops over actions, constructs models of outcomes that would follow from those actions, and outputs the action corresponding to the highest-ranked outcome is so that it is contradictory for the algorithm to output a suboptimal action.
This is what computer programs are all about. You write the code in such a fashion that the only non-contradictory way for the electricity to flow through the transistors is in the way that makes your computer do your tax returns, or whatever.
In the case of the XOR blackmail problem, there are four “possible” worlds: LT (letter + termites), NT (noletter + termites), LN (letter + notermites), and NN (noletter + notermites).
The predictor, by dint of their accuracy, has put the universe into a state where the only consistent possibilities are either (LT, NN) or (LN, NT). You get to choose which of those pairs is consistent and which is contradictory. Clearly, you don’t have control over the probability of termites vs. notermites, so you’re only controlling whether you get the letter. Thus, the question is whether you’re willing to pay $1000 to make sure that the letter shows up only in the worlds where you don’t have termites.
Even when you’re holding the letter in your hands, I claim that you should not say “if I pay I will have no termites”, because that is false — your action can’t affect whether you have termites. You should instead say:
I see two possibilities here. If my algorithm outputs pay, then in the XX% of worlds where I have termites I get no letter and lose $1M, and in the (100-XX)% of worlds where I do not have termites I lose $1k. If instead my algorithm outputs refuse, then in the XX% of worlds where I have termites I get this letter but only lose $1M, and in the other worlds I lose nothing. The latter mixture is preferable, so I do not pay.
You’ll notice that the agent in this line of reasoning is not updating on the fact that they’re holding the letter. They’re not saying, “Given that I know that I received the letter and that the universe is consistent…”
One way to think about this is to imagine the agent as not yet being sure whether or not they’re in a contradictory universe. They act like this might be a world in which they don’t have termites, and they received the letter; and in those worlds, by refusing to pay, they make the world they inhabit inconsistent — and thereby make this very scenario never-have-existed.
And this is correct reasoning! For when the predictor makes their prediction, they’ll visualize a scenario where the agent has no termites and receives the letter, in order to figure out what the agent would do. When the predictor observes that the agent would make that universe contradictory (by refusing to pay), they are bound (by their own commitments, and by their accuracy as a predictor) to send the letter only when you have termites. ((Ben Levinstein notes that this can be compared to backward induction in game theory with common knowledge of rationality. You suppose you’re at some final decision node which you only would have gotten to (as it turns out) if the players weren’t actually rational to begin with.))
You’ll never find yourself in a contradictory situation in the real world, but when an accurate predictor is trying to figure out what you’ll do, they don’t yet know which situations are contradictory. They’ll therefore imagine you in situations that may or may not turn out to be contradictory (like “letter + notermites”). Whether or not you would force the contradiction in those cases determines how the predictor will behave towards you in fact.
The real world is never contradictory, but predictions about you can certainly place you in contradictory hypotheticals. In cases where you want to force a certain hypothetical world to imply a contradiction, you have to be the sort of person who would force the contradiction if given the opportunity.
Or as I like to say — forcing the contradiction never works, but it always would’ve worked, which is sufficient.
Anonymous: The FDT algorithm is best ex ante. But if what you care about is your utility in your own life flowing after you, and not that of other instantiations, then upon hearing this news about FDT you should do whatever is best for you given that information and your beliefs, as per CDT.
Nate: If you have the ability to commit yourself to future behaviors (and actually stick to that), it’s clearly in your interest to commit now to behaving like FDT on all decision problems that begin in your future. I, for instance, have made this commitment myself. I’ve also made stronger commitments about decision problems that began in my past, but all CDT agents should agree in principle on problems that begin in the future. ((Specifically, the CDT-endorsed response here is: “Well, I’ll commit to acting like an FDT agent on future problems, but in one-shot prisoner’s dilemmas that began in my past, I’ll still defect against copies of myself”.
The problem with this response is that it can cost you arbitrary amounts of utility, provided a clever blackmailer wishes to take advantage. Consider the retrocausal blackmail dilemma in “Toward Idealized Decision Theory“:
There is a wealthy intelligent system and an honest AI researcher with access to the agent’s original source code. The researcher may deploy a virus that will cause $150 million each in damages to both the AI system and the researcher, and which may only be deactivated if the agent pays the researcher $100 million. The researcher is risk-averse and only deploys the virus upon becoming confident that the agent will pay up. The agent knows the situation and has an opportunity to self-modify after the researcher acquires its original source code but before the researcher decides whether or not to deploy the virus. (The researcher knows this, and has to factor this into their prediction.)
CDT pays the retrocausal blackmailer, even if it has the opportunity to precommit to do otherwise. FDT (which in any case has no need for precommitment mechanisms) refuses to pay. I cite the intuitive undesirability of this outcome to argue that one should follow FDT in full generality, as opposed to following CDT’s prescription that one should only behave in FDT-like ways in future dilemmas.
The argument above must be made from a pre-theoretic vantage point, because CDT is internally consistent. There is no argument one could give to a true CDT agent that would cause it to want to use anything other than CDT in decision problems that began in its past.
If examples like retrocausal blackmail have force (over and above the force of other arguments for FDT), it is because humans aren’t genuine CDT agents. We may come to endorse CDT based on its theoretical and practical virtues, but the case for CDT is defeasible if we discover sufficiently serious flaws in CDT, where “flaws” are evaluated relative to more elementary intuitions about which actions are good or bad. FDT’s advantages over CDT and EDT — properties like its greater theoretical simplicity and generality, and its achievement of greater utility in standard dilemmas — carry intuitive weight from a position of uncertainty about which decision theory is correct.))
I do believe that real-world people like you and me can actually follow FDT’s prescriptions, even in cases where those prescriptions are quite counter-intuitive.
Consider a variant of Newcomb’s problem where both boxes are transparent, so that you can already see whether box B is full before choosing whether to two-box. In this case, EDT joins CDT in two-boxing, because one-boxing can no longer serve to give the agent good news about its fortunes. But FDT agents still one-box, for the same reason they one-box in Newcomb’s original problem and cooperate in the prisoner’s dilemma: they imagine their algorithm controlling all instances of their decision procedure, including the past copy in the mind of their predictor.
Now, let’s suppose that you’re standing in front of two full boxes in the transparent Newcomb problem. You might say to yourself, “I wish I could have committed beforehand, but now that the choice is before me, the tug of the extra $1000 is just too strong”, and then decide that you were not actually capable of making binding precommitments. This is fine; the normatively correct decision theory might not be something that all human beings have the willpower to follow in real life, just as the correct moral theory could turn out to be something that some people lack the will to follow. ((In principle, it could even turn out that following the prescriptions of the correct decision theory in full generality is humanly impossible. There’s no law of logic saying that the normatively correct decision-making behaviors have to be compatible with arbitrary brain designs (including human brain design). I wouldn’t bet on this, but in such a case learning the correct theory would still have practical import, since we could still build AI systems to follow the normatively correct theory.))
That said, I believe that I’m quite capable of just acting like I committed to act. I don’t feel a need to go through any particular mental ritual in order to feel comfortable one-boxing. I can just decide to one-box and let the matter rest there.
I want to be the kind of agent that sees two full boxes, so that I can walk away rich. I care more about doing what works, and about achieving practical real-world goals, than I care about the intuitiveness of my local decisions. And in this decision problem, FDT agents are the only agents that walk away rich.
One way of making sense of this kind of reasoning is that evolution graced me with a “just do what you promised to do” module. The same style of reasoning that allows me to actually follow through and one-box in Newcomb’s problem is the one that allows me to cooperate in prisoner’s dilemmas against myself — including dilemmas like “should I stick to my New Year’s resolution?” ((A New Year’s resolution that requires me to repeatedly follow through on a promise that I care about in the long run, but would prefer to ignore in the moment, can be modeled as a one-shot twin prisoner’s dilemma. In this case, the dilemma is temporally extended, and my “twins” are my own future selves, who I know reason more or less the same way I do.
It’s conceivable that I could go off my diet today (“defect”) and have my future selves pick up the slack for me and stick to the diet (“cooperate”), but in practice if I’m the kind of agent who isn’t willing today to sacrifice short-term comfort for long-term well-being, then I presumably won’t be that kind of agent tomorrow either, or the day after.
Seeing that this is so, and lacking a way to force themselves or their future selves to follow through, CDT agents despair of promise-keeping and abandon their resolutions. FDT agents, seeing the same set of facts, do just the opposite: they resolve to cooperate today, knowing that their future selves will reason symmetrically and do the same.)) I claim that it was only misguided CDT philosophers that argued (wrongly) that “rational” agents aren’t allowed to use that evolution-given “just follow through with your promises” module.
Anonymous: A final point: I don’t know about counterlogicals, but a theory of functional similarity would seem to depend on the details of the algorithms.
E.g., we could have a model where their output is stochastic, but some parameters of that process are the same (such as expected value), and the action is stochastically drawn from some distribution with those parameter values. We could have a version of that, but where the parameter values depend on private information picked up since the algorithms split, in which case each agent would have to model the distribution of private info the other might have.
That seems pretty general; does that work? Is there a class of functional similarity that can not be expressed using that formulation?
Nate: As long as the underlying distribution can be an arbitrary Turing machine, I think that’s sufficiently general.
There are actually a few non-obvious technical hurdles here; namely, if agent A is basing their beliefs off of their model of agent B, who is basing their beliefs off of a model of agent A, then you can get some strange loops.
Consider for example the matching pennies problem: agent A and agent B will each place a penny on a table; agent A wants either HH or TT, and agent B wants either HT or TH. It’s non-trivial to ensure that both agents develop stable accurate beliefs in games like this (as opposed to, e.g., diving into infinite loops).
The technical solution to this is reflective oracle machines, a class of probabilistic Turing machines with access to an oracle that can probabilistically answer questions about any other machine in the class (with access to the same oracle).
The paper “Reflective Oracles: A Foundation for Classical Game Theory” shows how to do this and shows that the relevant fixed points always exist. (And furthermore, in cases that can be represented in classical game theory, the fixed points always correspond to the mixed-strategy Nash equilibria.)
This more or less lets us start from a place of saying “how do agents with probabilistic information about each other’s source code come to stable beliefs about each other?” and gets us to the “common knowledge of rationality” axiom from game theory. ((The paper above shows how to use reflective oracles with CDT as opposed to FDT, because (a) one battle at a time and (b) we don’t yet have a generic algorithm for computing logical counterfactuals, but we do have a generic algorithm for doing CDT-type reasoning.)) One can also see it as a justification for that axiom, or as a generalization of that axiom that works even in cases where the lines between agent and environment get blurry, or as a hint at what we should do in cases where one agent has significantly more computational resources than the other, etc.
But, yes, when we study these kinds of problems concretely at MIRI, we tend to use models where each agent models the other as a probabilistic Turing machine, which seems roughly in line with what you’re suggesting here.