MIRI’s mission is “to ensure that the creation of smarter-than-human artificial intelligence has a positive impact.” How can we ensure any such thing? It’s a daunting task, especially given that we don’t have any smarter-than-human machines to work with at the moment. In the previous post I discussed four background claims that motivate our mission; in this post I will describe our approach to addressing the challenge.
This challenge is sizeable, and we can only tackle a portion of the problem. For this reason, we specialize. Our two biggest specializing assumptions are as follows:
We focus on scenarios where smarter-than-human machine intelligence is first created in de novo software systems (as opposed to, say, brain emulations).
This is in part because it seems difficult to get all the way to brain emulation before someone reverse-engineers the algorithms used by the brain and uses them in a software system, and in part because we expect that any highly reliable AI system will need to have at least some components built from the ground up for safety and transparency. Nevertheless, it is quite plausible that early superintelligent systems will not be human-designed software, and I strongly endorse research programs that focus on reducing risks along the other pathways.
We specialize almost entirely in technical research.
We select our researchers for their proficiency in mathematics and computer science, rather than forecasting expertise or political acumen. I stress that this is only one part of the puzzle: figuring out how to build the right system is useless if the right system does not in fact get built, and ensuring AI has a positive impact is not simply a technical problem. It is also a global coordination problem, in the face of short-term incentives to cut corners. Addressing these non-technical challenges is an important task that we do not focus on.
In short, MIRI does technical research to ensure that de novo AI software systems will have a positive impact. We do not further discriminate between different types of AI software systems, nor do we make strong claims about exactly how quickly we expect AI systems to attain superintelligence. Rather, our current approach is to select open problems using the following question:
What would we still be unable to solve, even if the challenge were far simpler?
For example, we might study AI alignment problems that we could not solve even if we had lots of computing power and very simple goals.
We then filter on problems that are (1) tractable, in the sense that we can do productive mathematical research on them today; (2) uncrowded, in the sense that the problems are not likely to be addressed during normal capabilities research; and (3) critical, in the sense that they could not be safely delegated to a machine unless we had first solved them ourselves. (Since the goal is to design intelligent machines, there are many technical problems that we can expect to eventually delegate to those machines. But it is difficult to trust an unreliable reasoner with the task of designing reliable reasoning!)
These three filters are usually uncontroversial. The controversial claim here is that the above question — “what would we be unable to solve, even if the challenge were simpler?” — is a generator of open technical problems for which solutions will help us design safer and more reliable AI software in the future, regardless of their architecture. The rest of this post is dedicated to justifying this claim, and describing the reasoning behind it.
1. Creating a powerful AI system without understanding why it works is dangerous.
A large portion of the risk from machine superintelligence comes from the possibility of people building systems that they do not fully understand.
Currently, this is commonplace in practice: many modern AI researchers are pushing the capabilities of deep neural networks in the absence of theoretical foundations that describe why they’re working so well or a solid idea of what goes on beneath the hood. These shortcomings are being addressed over time: many AI researchers are currently working on transparency tools for neural networks, and many more are working to put theoretical foundations beneath deep learning systems. In the interim, using trial and error to push the capabilities of modern AI systems has led to many useful applications.
When designing a superintelligent agent, by contrast, we will want an unusually high level of confidence in its safety before we begin online testing: trial and error alone won’t cut it, in that domain.
To illustrate, consider a study by Bird and Layzell in 2002. They used some simple genetic programming to design an oscillating circuit on a circuit board. One solution that the genetic algorithm found entirely avoided using the built-in capacitors (an essential piece of hardware in human-designed oscillators). Instead, it repurposed the circuit tracks on the motherboard as a radio receiver, and amplified an oscillating signal from a nearby computer.
This demonstrates that powerful search processes can often reach their goals via unanticipated paths. If Bird and Layzell were hoping to use their genetic algorithm to find code for a robust oscillating circuit — one that could be used on many different circuit boards regardless of whether there were other computers present — then they would have been sorely disappointed. Yet if they had tested their algorithms extensively on a virtual circuit board that captured all the features of the circuit board that they thought were relevant (but not features such as “circuit tracks can carry radio signals”), then they would not have noticed the potential for failure during testing. If this is a problem when handling simple genetic search algorithms, then it will be a much larger problem when handling smarter-than-human search processes.
When it comes to designing smarter-than-human machine intelligence, extensive testing is essential, but not sufficient: in order to be confident that the system will not find unanticipated bad solutions when running in the real world, it is important to have a solid understanding of how the search process works and why it is expected to generate only satisfactory solutions in addition to empirical test data.
MIRI’s research program is aimed at ensuring that we have the tools needed to inspect and analyze smarter-than-human search processes before we deploy them.
By analogy, neural net researchers could probably have gotten quite far without having any formal understanding of probability theory. Without probability theory, however, they would lack the tools needed to understand modern AI algorithms: they wouldn’t know about Bayes nets, they wouldn’t know how to formulate assumptions like “independent and identically distributed,” and they wouldn’t quite know the conditions under which Markov Decision Processes work and fail. They wouldn’t be able to talk about priors, or check for places where the priors are zero (and therefore identify things that their systems cannot learn). They wouldn’t be able to talk about bounds on errors and prove nice theorems about algorithms that find an optimal policy eventually.
They probably could have still gotten pretty far (and developed half-formed ad-hoc replacements for many of these ideas), but without probability theory, I expect they would have a harder time designing highly reliable AI algorithms. Researchers at MIRI tend to believe that similarly large chunks of AI theory are still missing, and those are the tools that our research program aims to develop.
2. We could not yet create a beneficial AI system even via brute force.
Imagine you have a Jupiter-sized computer and a very simple goal: Make the universe contain as much diamond as possible. The computer has access to the internet and a number of robotic factories and laboratories, and by “diamond” we mean carbon atoms covalently bound to four other carbon atoms. (Pretend we don’t care how it makes the diamond, or what it has to take apart in order to get the carbon; the goal is to study a simplified problem.) Let’s say that the Jupiter-sized computer is running python. How would you program it to produce lots and lots of diamond?
As it stands, we do not yet know how to program a computer to achieve a goal such as that one.
We couldn’t yet create an artificial general intelligence by brute force, and this indicates that there are parts of the problem we don’t yet understand.
There are a number of AI tasks that we could brute-force. For example, we could write a program that would be really, really good at solving computer vision problems: if we had an indestructible box that produced pictures and questions about them, waited for answers, scored the answers for accuracy, and then repeated the process, then we know how to write the program that interacts with that box and gets very good at answering the questions. (The program would essentially be a bounded version of AIXI.)
By a similar method, if we had an indestructible box that produced a conversation and questions about it, waited for natural-language answers to the questions, and scored them for accuracy, then again, we could write a program that would get very good at answering well. In this sense, we know how to solve computer vision and natural language processing by brute force. (Of course, natural-language processing is nowhere near “solved” in a practical sense — there is still loads of work to be done. A brute force solution doesn’t get you very far in the real world. The point is that, for many AI alignment problems, we haven’t even made it to the “we could brute force it” level yet.)
Why do we need the indestructible box in the above examples? Because the way the modern brute-force solution would work is by considering each Turing machine (up to some complexity limit) as a hypothesis about the box, seeing which ones are consistent with observation, and then executing actions that lead to high scores coming out of the box (as predicted by the remaining hypotheses, weighted by simplicity).
Each hypothesis is an opaque Turing machine, and the algorithm never peeks inside: it just asks each hypothesis to predict what score the box will output if it executes a certain action chain. This means that if the algorithm finds (via exhaustive search) a plan that maximizes the score coming out of the box, and the box is destructible, then the opaque action chain that maximizes score is very likely to be the one that pops the box open and alters it so that it always outputs the highest score. But given an indestructible box, we know how to brute force the answers.
In fact, roughly speaking, we understand how to solve any reinforcement learning problem via brute force. This is a far cry from knowing how to practically solve reinforcement learning problems! But it does illustrate a difference in kind between two types of problems. We can (imperfectly and heuristically) divide AI problems up as follows:
There are two types of open problem in AI. One is figuring how to solve in practice problems that we know how to solve in principle. The other is figuring out how to solve in principle problems that we don’t even know how to brute force yet.
MIRI focuses on problems of the second class.1
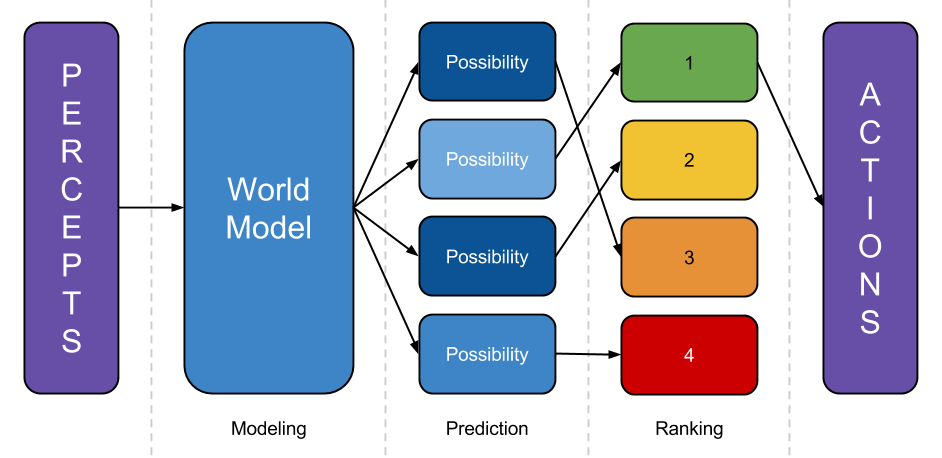
What is hard about brute-forcing a diamond-producing agent? To illustrate, I’ll give a wildly simplified sketch of what an AI program needs to do in order to act productively within a complex environment:
- Model the world: Take percepts, and use them to refine some internal representation of the world the system is embedded in.
- Predict the world: Take that world-model, and predict what would happen if the system executed various different plans.
- Rank outcomes: Rate those possibilities by how good the predicted future is, then execute a plan that leads to a highly-rated outcome.2
Consider the modeling step. As discussed above, we know how to write an algorithm that finds good world-models by brute force: it looks at lots and lots of Turing machines, weighted by simplicity, treats them like they are responsible for its observations, and throws out the ones that are inconsistent with observation thus far. But (aside from being wildly impractical) this yields only opaque hypotheses: the system can ask what “sensory bits” each Turing machine outputs, but it cannot peek inside and examine objects represented within.
If there is some well-defined “score” that gets spit out by the opaque Turing machine (as in a reinforcement learning problem), then it doesn’t matter that each hypothesis is a black box; the brute-force algorithm can simply run the black box on lots of inputs and see which results in the highest score. But if the problem is to build lots of diamond in the real world, then the agent must work as follows:
- Build a model of the world — one that represents carbon atoms and covalent bonds, among other things.
- Predict how the world would change contingent on different actions the system could execute.
- Look inside each prediction and see which predicted future has the most diamond. Execute the action that leads to more diamond.
In other words, an AI that is built to reliably affect things in the world needs to have world-models that are amenable to inspection. The system needs to be able to pop open the world model, identify the representations of carbon atoms and covalent bonds, and estimate how much diamond is in the real world.3
We don’t yet have a clear picture of how to build “inspectable” world-models — not even by brute force. Imagine trying to write the part of the diamond-making program that builds a world-model: this function needs to take percepts as input and build a data structure that represents the universe, in a way that allows the system to inspect universe-descriptions and estimate the amount of diamond in a possible future. Where in the data structure are the carbon atoms? How does the data structure allow the concept of a “covalent bond” to be formed and labeled, in such a way that it remains accurate even as the world-model stops representing diamond as made of atoms and starts representing them as made of protons, neutrons, and electrons instead?
We need a world-modeling algorithm that builds multi-level representations of the world and allows the system to pursue the same goals (make diamond) even as its model changes drastically (because it discovers quantum mechanics). This is in stark contrast to the existing brute-force solutions that use opaque Turing machines as hypotheses.4
When humans reason about the universe, we seem to do some sort of reasoning outwards from the middle: we start by modeling things like people and rocks, and eventually realize that these are made of atoms, which are made of protons and neutrons and electrons, which are perturbations in quantum fields. At no point are we certain that the lowest level in our model is the lowest level in reality; as we continue thinking about the world we construct new hypotheses to explain oddities in our models. What sort of data structure are we using, there? How do we add levels to a world model given new insights? This is the sort of reasoning algorithm that we do not yet understand how to formalize.5
That’s step one in brute-forcing an AI that reliably pursues a simple goal. We also don’t know how to brute-force steps two or three yet. By simplifying the problem — talking about diamonds, for example, rather than more realistic goals that raise a host of other difficulties — we’re able to factor out the parts of the problems that we don’t understand how to solve yet, even in principle. Our technical agenda describes a number of open problems identified using this method.
3. Figuring out how to solve a problem in principle yields many benefits.
In 1836, Edgar Allen Poe wrote a wonderful essay on Maelzel’s Mechanical Turk, a machine that was purported to be able to play chess. In the essay, Poe argues that the Mechanical Turk must be a hoax: he begins by arguing that machines cannot play chess, and proceeds to explain (using his knowledge of stagecraft) how a person could be hidden within the machine. Poe’s essay is remarkably sophisticated, and a fun read: he makes reference to the “calculating machine of Mr. Babbage” and argues that it cannot possibly be made to play chess, because in a calculating machine, each steps follows from the previous step by necessity, whereas “no one move in chess necessarily follows upon any one other”.
The Mechnical Turk indeed turned out to be a hoax. In 1950, however, Claude Shannon published a rather compelling counterargument to Poe’s reasoning in the form of a paper explaining how to program a computer to play perfect chess.
Shannon’s algorithm was by no means the end of the conversation. It took forty-six years to go from that paper to Deep Blue, a practical chess program which beat the human world champion. Nevertheless, if you were equipped with Poe’s state of knowledge and not yet sure whether it was possible for a computer to play chess — because you did not yet understand algorithms for constructing game trees and doing backtracking search — then you would probably not be ready to start writing practical chess programs.
Similarly, if you lacked the tools of probability theory — an understanding of Bayesian inference and the limitations that stem from bad priors — then you probably wouldn’t be ready to program an AI system that needed to manage uncertainty in high-stakes situations.
If you are trying to write a program and you can’t yet say how you would write it given an arbitrarily large computer, then you probably aren’t yet ready to design a practical approximation of the brute-force solution yet. Practical chess programs can’t generate a full search tree, and so rely heavily on heuristics and approximations; but if you can’t brute-force the answer yet given arbitrary amounts of computing power, then it’s likely that you’re missing some important conceptual tools.
Marcus Hutter (inventor of AIXI) and Shane Legg (inventor of the Universal Measure of Intelligence) seem to endorse this approach. Their work can be interpreted as a description of how to find a brute-force solution to any reinforcement learning problem, and indeed, the above description of how to do this is due to Legg and Hutter.
In fact, the founders of Google DeepMind reference the completion of Shane’s thesis as one of four key indicators that the time was ripe to begin working on AGI: a theoretical framework describing how to solve reinforcement learning problems in principle demonstrated that modern understanding of the problem had matured to the point where it was time for the practical work to begin.
Before we gain a formal understanding of the problem, we can’t be quite sure what the problem is. We may fail to notice holes in our reasoning; we may fail to bring the appropriate tools to bear; we may not be able to tell when we’re making progress. After we gain a formal understanding of the problem in principle, we’ll be in a better position to make practical progress.
The point of developing a formal understanding of a problem is not to run the resulting algorithms. Deep Blue did not work by computing a full game tree, and DeepMind is not trying to implement AIXI. Rather, the point is to identify and develop the basic concepts and methods that are useful for solving the problem (such as game trees and backtracking search algorithms, in the case of chess).
The development of probability theory has been quite useful to the field of AI — not because anyone goes out and attempts to build a perfect Bayesian reasoner, but because probability theory is the unifying theory for reasoning under uncertainty. This makes the tools of probability theory useful for AI designs that vary in any number of implementation details: any time you build an algorithm that attempts to manage uncertainty, a solid understanding of probabilistic inference is helpful when reasoning about the domain in which the system will succeed and the conditions under which it could fail.
This is why we think we can identify open problems that we can work on today, and which will reliably be useful no matter how the generally intelligent machines of the future are designed (or how long it takes to get there). By seeking out problems that we couldn’t solve even if the problem were much easier, we hope to identify places where core AGI algorithms are missing. By developing a formal understanding of how to address those problems in principle, we aim to ensure that when it comes time to address those problems in practice, programmers have the knowledge they need to develop solutions that they deeply understand, and the tools they need to ensure that the systems they build are highly reliable.
4. This is an approach researchers have used successfully in the past.
Our main open-problem generator — “what would we be unable to solve even if the problem were easier?” — is actually a fairly common one used across mathematics and computer science. It’s more easy to recognize if we rephrase it slightly: “can we reduce the problem of building a beneficial AI to some other, simpler problem?”
For example, instead of asking whether you can program a Jupiter-sized computer to produce diamonds, you could rephrase this as a question about whether we can reduce the diamond maximization problem to known reasoning and planning procedures. (The current answer is “not yet.”)
This is a fairly standard practice in computer science, where reducing one problem to another is a key feature of computability theory. In mathematics it is common to achieve a proof by reducing one problem to another (see, for instance, the famous case of Fermat’s last theorem). This helps one focus on the parts of the problem that aren’t solved, and identify topics where foundational understanding is lacking.
As it happens, humans have a pretty good track record when it comes to working on problems such as these. Humanity hasn’t been very good at predicting long-term technological trends, but we have reasonable success developing theoretical foundations for technical problems decades in advance, when we put sufficient effort into it. Alan Turing and Alonzo Church succeeded in developing a robust theory of computation that proved quite useful once computers were developed, in large part by figuring out how to solve (in principle) problems which they did not yet know how to solve with machines. Andrey Kolmogorov, similarly, set out to formalize intuitive but not-yet-well-understood methods for managing uncertainty; and he succeeded. And Claude Shannon and his contemporaries succeeded at this endeavor in the case of chess.
The development of probability theory is a particularly good analogy to our case: it is a field where, for hundreds of years, philosophers and mathematicians who attempted to formalize their intuitive notions of “uncertainty” repeatedly reasoned themselves into paradoxes and contradictions. The probability theory at the time, sorely lacking formal foundations, was dubbed a “theory of misfortune.” Nevertheless, a concerted effort by Kolmogorov and others to formalize the theory was successful, and his efforts inspired the development of a host of useful tools for designing systems that reason reliably under uncertainty.
Many people who set out to put foundations under a new field of study (that was intuitively understood on some level but not yet formalized) have succeeded, and their successes have been practically significant. We aim to do something similar for a number of open problems pertaining to the design of highly reliable reasoners.
The questions MIRI focuses on, such as “how would one ideally handle logical uncertainty?” or “how would one ideally build multi-level world models of a complex environment?”, exist at a level of generality comparable to Kolmogorov’s “how would one ideally handle empirical uncertainty?” or Hutter’s “how would one ideally maximize reward in an arbitrarily complex environment?” The historical track record suggests that these are the kinds of problems that it is possible to both (a) see coming in advance, and (b) work on without access to a concrete practical implementation of a general intelligence.
By identifying parts of the problem that we would still be unable to solve even if the problem was easier, we hope to hone in on parts of the problem where core algorithms and insights are missing: algorithms and insights that will be useful no matter what architecture early intelligent machines take on, and no matter how long it takes to create smarter-than-human machine intelligence.
At present, there are only three people on our research team, and this limits the number of problems that we can tackle ourselves. But our approach is one that we can scale up dramatically: it has generated a very large number of open problems, and we have no shortage of questions to study.6
This is an approach that has often worked well in the past for humans trying to understand how to approach a new field of study, and I am confident that this approach is pointing us towards some of the core hurdles in this young field of AI alignment.
- Most of the AI field focuses on problems of the first class. Deep learning, for example, is a very powerful and exciting tool for solving problems that we know how to brute-force, but which were, up until a few years ago, wildly intractable. Class 1 problems tend to be important problems for building more capable AI systems, but lower-priority for ensuring that highly capable systems are aligned with our interests. ↩
- In reality, of course, there aren’t clean separations between these steps. The “prediction” step must be more of a ranking-dependent planning step, to avoid wasting computation predicting outcomes that will obviously be poorly-ranked. The modeling step depends on the prediction step, because which parts of the world-model are refined depends on what the world-model is going to be used for. A realistic agent would need to make use of meta-planning to figure out how to allocate resources between these activities, etc. This diagram is a fine first approximation, though: if a system doesn’t do something like modeling the world, predicting outcomes, and ranking them somewhere along the way, then it will have a hard time steering the future. ↩
- In reinforcement learning problems, this issue is avoided via a special “reward channel” intended to stand in indirectly for something the supervisor wants. (For example, the supervisor may push a reward button every time the learner takes an action that seems, to the supervisor, to be useful for making diamonds.) Then the programmers can, by hand, single out the reward channel inside the world-model and program the system to execute actions that it predicts lead to high reward. This is much easier than designing world-models in such a way that the system can reliably identify representations of carbon atoms and covalent bonds within it (especially if the world is modeled in terms of Newtonian mechanics one day and quantum mechanics the next), but doesn’t provide a framework for agents that must autonomously learn how to achieve some goal. Correct behavior in highly intelligent systems will not always be reducible to maximizing a reward signal controlled by a significantly less intelligent system (e.g., a human supervisor). ↩
- The idea of a search algorithm that optimizes according to modeled facts about the world rather than just expected percepts may sound basic, but we haven’t found any deep insights (or clever hacks) that allow us to formalize this idea (e.g., as a brute-force algorithm). If we could formalize it, we would likely get a better understanding of the kind of abstract modeling of objects and facts that is required for self-referential, logically uncertain, programmer-inspectable reasoning. ↩
- We also suspect that a brute-force algorithm for building multi-level world models would be much more amenable to being “scaled down” than Solomonoff induction, and would therefore lend some insight into how to build multi-level world models in a practical setting. ↩
- For example, instead of asking what problems remain when given lots of computing power, you could instead ask whether we can reduce the problem of building an aligned AI to the problem of making reliable predictions about human behavior: an approach advocated by others. ↩
Did you like this post? You may enjoy our other Analysis posts, including:
