Bas Steunebrink is a postdoctoral researcher at the Swiss AI lab IDSIA, as part of Prof. Schmidhuber’s group. He received his PhD in 2010 from Utrecht University, the Netherlands. Bas’s dissertation was on the subject of artificial emotions, which fits well in his continuing quest of finding practical and creative ways in which general intelligent agents can deal with time and resource constraints. A recent paper on how such agents will naturally strive to be effective, efficient, and curious was awarded the Kurzweil Prize for Best AGI Idea at AGI’2013. Bas also has a great interest in anything related to self-reflection and meta-learning, and all “meta” stuff in general.
Luke Muehlhauser: One of your ongoing projects has been a Gödel machine (GM) implementation. Could you please explain (1) what a Gödel machine is, (2) why you’re motivated to work on that project, and (3) what your implementation of it does?
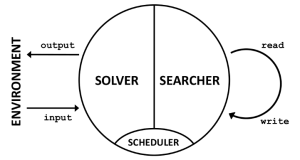
Bas Steunebrink: A GM is a program consisting of two parts running in parallel; let’s name them Solver and Searcher. Solver can be any routine that does something useful, such as solving task after task in some environment. Searcher is a routine that tries to find beneficial modifications to both Solver and Searcher, i.e., to any part of the GM’s software. So Searcher can inspect and modify any part of the Gödel Machine. The trick is that the initial setup of Searcher only allows Searcher to make such a self-modification if it has a proof that performing this self-modification is beneficial in the long run, according to an initially provided utility function. Since Solver and Searcher are running in parallel, you could say that a third component is necessary: a Scheduler. Of course Searcher also has read and write access to the Scheduler’s code.
In the old days, writing code that makes self-modifications was seen as a nice way of saving on memory, which was very expensive. But now that memory is cheap and making self-modifications has turned out to be error-prone, this technique has been mostly banished. Modern programming languages abstract away from internals and encapsulate them, such that more guarantees about safety and performance can be given. But now that the techniques for automated reasoning developed by the theorem proving and artificial intelligence communities are maturing, a new opportunity for self-reflection emerges: to let the machine itself do all the reasoning and decide when, where, and how to perform self-modifications.
The construction of an actual implementation of a Gödel Machine is currently ongoing work, and I’m collaborating and consulting with MIRI in this endeavor. The technical problem of obtaining a system with anytime self-reflection capabilities can be considered solved. This includes answering the nontrivial question of what it means to inspect the state and behavior of actively running, resource-constrained code, and how it can safely by modified, at any time. Current work focuses on encoding the operational semantics of the system within a program being run by the system. Although these operational semantics are extremely simple, there remain possible theoretical hurdles, such as the implications of Löb’s Theorem (Yudkowsky & Herreshoff 2013)
It will be interesting to see how well current Automated Theorem Provers (ATP) hold up in a Gödel Machine setting, because here we are trying to formulate proofs about code that is actively running, and which contains the ATP itself, and which is subject to resource constraints. There may be interesting lessons in here as well for the ATP developers and community.
Luke: You say that “the technical problem of obtaining a system with anytime self-reflection capabilities can be considered solved.” Could you give us a sketch of the solution to which you’re referring?
Bas: There are two issues at play here. First, there is the issue of deciding what you will see upon performing self-reflection. For example, we can ask whether a process can see the call stack of other currently running processes, or even its own call stack, and what operations can be performed on such a call stack to inspect and modify it. But second, performing self-reflection is an act in time: when a machine inspects (and modifies) its own internals, this happens at some moment in time, and doing so takes some time. The question here is, can the machine decide when to perform self-reflection?
We can envisage a machine which is performing duties by day, and every night at 2:00am is allowed access to several internal register to make adjustments based on the events of the past day, in order to be better prepared for the next day. One could argue that this machine has full self-reflective capabilities, because look, it can meddle around without restrictions every day. But it still lacks a certain degree of control, namely in time.
What I have done is design a mechanism by which a machine can decide with very high precision when it wants to inspect a certain process. It involves dividing the operation of the machine into extremely small blocks, with the possibility for interruption between any two blocks. On an average desktop this gives about 50 million opportunities for initiating self-reflection per second, which I think is fine-grained enough for the anytime label.
Besides the anytime issue of self-reflection, there are many other (technical) questions that have to be answered when implementing a self-reflective system such as a Gödel Machine. For example: should (self-)reflection interrupt the thing it is reflecting on, or can it look at something that is changing while you look at it? In an extreme case, you could be looking at your own call stack, where every probing instruction directly affects the thing being probed. Is this a powerful ability, or merely dangerous and stupid? In the self-reflective system that I have implemented, called Sleight, the default behavior is interruption, but the fluid case is very easy to get too, if you want. Basically, what it requires is interruption and immediate resumption, while saving a pointer to the obtained internal state of the resumed process. Now you can watch yourself change due to you watching yourself… It’s a bit like watching a very high-resolution, live brain scan of your own brain, but with the added ability of changing connectivity and activation anywhere at any time.
Luke: Another project you’ve been working on is called Sleight. What is Sleight, and what is its purpose?
Bas: Sleight is a self-reflective programming system. It consists of a compiler from Scheme to Sleight code, and a virtual machine (VM) for running Sleight code. The VM is what is called a self-reflective interpreter: it allows code being run to inspect and modify internal registers of the VM. These registers include the call stack and all variable assignments. Since all code is assigned to variables, Sleight code has complete access to its own source code at runtime. Furthermore, Sleight offers a mechanism for scheduling multiple processes. Of course, each process can inspect and modify other processes at any time. Protection and other safety issues have been well taken care of — although a process can easily cripple itself, the VM cannot be crashed.
The purpose of Sleight is to function as a platform for safely experimenting with self-reflective code, and for implementing a Gödel Machine in particular. The scheduling capabilities of the Sleight VM make it especially suitable for setting up the Solver, Searcher, and Scheduler — see the figure above.
Luke: A typical approach to reflective interpreters is the “reflective tower” of e.g. 3-Lisp (Rivieres & Smith 1984). Interestingly, Sleight collapses the reflective tower into what you call a “reflective bungalow.” Could you explain what this means, and why it’s a good idea?
Bas: The reflective tower is a construct that in theory is infinite in two directions, like a tower with no ground floor and no top floor. I love the following quote from Christian Queinnec on the concept:
In the mid-eighties, there was a fashion for reflective interpreters, a fad that gave rise to a remarkable term: “reflective towers.” Just imagine a marsh shrouded in mist and a rising tower with its summit lost in gray and cloudy skies—pure Rackham! […] Well, who hasn’t dreamed about inventing (or at least having available) a language where anything could be redefined, where our imagination could gallop unbridled, where we could play around in complete programming liberty without trammel nor hindrance?
The infinite reflective tower, as so poetically described by Queinnec in the quote above, can be visualized as an infinite nesting of interpreters, each interpreter being run by another interpreter. In the tower metaphor, each interpreter is being run by an interpreter one floor above it, and each interpreter can start running a new interpreter, adding a floor below itself. Going one floor up is then called reification, whereas going one floor down is called reflection. Theoretically the tower can be infinitely high, but in a practical implementation the tower must have a top, which is formed by a black-box interpreter whose internal state cannot be reified, as is the case in this pedagogical example. The point of having access to the interpreter running one floor up is that you can redefine any function and change your own operational semantics at will.
Yet I consider the theoretical ideal of the infinite tower not so ideal at all: if there is always more internal state that can be reified, ad infinitum, then the operational semantics of the machine as a whole must be unfounded or circular. But with a simple trick we can make do with just one interpreter and no nesting. We can do this by maintaining a special data structure: the metacontinuation. The metacontinuation is a “tower” or stack of interpreter states. The act of reification, which in the infinite tower meant moving one floor up, now means popping one interpreter state off the metacontinuation, and running the sole interpreter using that state. Likewise, the act of reflection, which in the infinite tower meant adding a floor below, now means pushing the current interpreter state onto the metacontinuation. This way we can imitate the effect of an infinite tower of interpreters without any need for nesting—it just needs an extra stack, effectively becoming a “reflective bungalow.”
Although the metacontinuation is not an invention of mine—see also “Brown” (Friedman & Wand, 1984; Wand & Friedman, 1986) and “Blond” (Danvy & Malmkjær, 1988)—there is a whole lot of fun to be had with it. For example, in Sleight, I have extended the metacontinuation concept with an extremely fine-grained interruption mechanism, such that self-reflection can be performed at any time. It also facilitates the implementation of schedulers for “green” threads, which is helpful for a Gödel Machine implementation.
Luke: Some of MIRI’s research frames questions of self-reflection in terms of successor agents (e.g. Yudkowsky & Herreshoff 2013). You might call this ex-vivo self-modification vs. Sleight’s more in-vivo methods (reflecting on oneself in real-time). What are the benefits from operating in the in-vivo framework vs an ex-vivo one?
Bas: It seems to me that there are two ways to look at the in-vivo versus ex-vivo frameworks: with respect to inspection and with respect to modification.
An agent with in-vivo inspection capabilities may be said to have read access to its own actual internal registers, whereas an agent with ex-vivo inspection capabilities may only be able to request occasional snapshots (copies) of its internal registers to be made available for inspection. In the in-vivo inspection case, the very act of inspection is likely to change the thing being inspected, whereas in the ex-vivo inspection case, the agent is looking at a static object. The latter is probably easier to deal with, although the two capabilities are very different. Sleight supports both though.
The cited paper, however, deals with ex-vivo modification capabilities, meaning that self-modifications are made to a copy of the agent. This is reminiscent of an agent producing fitter offspring. As I understand it, the ex-vivo modification method is a generalization of in-vivo modification, promising to create an elegant formal framework of investigation. But when an agent is studying its own workings in order to find a beneficial ex-vivo modification to it, is this done using in-vivo or ex-vivo inspection? These different inspection methods may yield very different results, so I think this question also deserves investigation. Personally I think the in-vivo frameworks are the most interesting (if only because of their difficulty and danger…), but it remains to be seen which will work best in practice, which is what counts eventually.
Luke: Sorry, what do you mean by this statement? “I think the in-vivo frameworks are the most interesting (if only because of their difficulty and danger)…”
Bas: The difficulty is in the in-vivo inspection: a common assumption made by automated reasoning techniques is that the data being reasoned about is static while the reasoning is in progress. But if the data includes the dynamic internal state of the reasoner, this assumption breaks down. I find this interesting because we are entering uncharted territory.
The danger is in the in-vivo modification: if an agent decides to modify its own software, there may be no way back. The agent must be very sure what it is doing, or it might end up disabling itself. Although, come to think of it, the ex-vivo modification — i.e., producing a successor agent — comes with its own dangers. For example, it may be technically impossible to halt a flawed yet powerful successor agent, or it may be unethical to do so.
Luke: You say that “if an agent decides to modify its own software, it must be very sure what it is doing, or it might end up disabling itself.” Presumably another worry, from both the perspective of the agent and that of its creators, is that a self-modification may result in unintended consequences for the agent’s future behavior.
Ideally, we’d want an agent to continue pursuing the same ends, with the same constraints on its behavior, even as it modifies itself (to become capable of achieving its goals more effectively and efficiently). That is, we want a solution to the problem of what we might call “stable self-modification.”
Besides Yudkowsky & Herreschoff (2013), are you aware of other literature on the topic? And what are your thoughts on the challenge of stable self-modification?
Bas: This is a very interesting question, which I think concerns the issue of growth in general. It seems to me there are actually two questions here: (1) How can an agent be constructed such that it can grow stably from a “seed” program? And (2) How much supervision, testing, corrections, and interventions does such an agent need while it is growing?
The first question assumes that handcrafting a complex AI system is very hard and a bad strategy anyway — something which we will not have to argue over, I think. A great exploration of the prerequisites for stable self-growth has been performed by Kristinn Thórisson (2012) from Reykjavik University, who labels the approach of building self-growing systems Constructivist AI. I have had (and still have) the pleasure of working with him during the EU-funded HumanObs project, where we implemented a comprehensive cognitive architecture satisfying the prerequisites for stable self-growth and following the constructivist methodology laid out in the linked paper. The architecture is called AERA and is based on the Replicode programming platform (developed mostly by Eric Nivel). This stuff is still very much work-in-progress, with a bunch of papers on AERA currently in preparation. So yes, I believe there exists a way of achieving long-term stable self-growth, and we are actively pursuing a promising path in this direction with several partner institutes.
The second question is an age-old one, especially regarding our own children, with our answers determining our schooling system. But many AI researcher seem to aim for a purely “intellectual” solution to the problem of building intelligent agents. For example, one could spend some time in front of a computer, programming a Gödel Machine or other “ultimate algorithm”, run it, sit back, and just wait for it to launch us all into the singularity… But I’m not too optimistic it will work out this way. I think we may have to get up and take a much more parental and social approach to crafting AI systems. To ensure stable growth, we may have to spend lots of time interacting with our creations, run occasional tests, like with school tests for children, and apply corrections if necessary. It will not be the rising of the machines, but rather the raising of the machines.
I’m hedging my bets though, by working on both sides simultaneously: AERA and the constructivist methodology on the one hand, and the Gödel Machine and other “ultimate” learning algorithms on the other hand.
Luke: Thanks, Bas!
Did you like this post? You may enjoy our other Conversations posts, including:
