Max Tegmark on the mathematical universe

Luke Muehlhauser: Your book opens with a concise argument against the absurdity heuristic — the rule of thumb which says “If a theory sounds absurd to my human psychology, it’s probably false.” You write:

Evolution endowed us with intuition only for those aspects of physics that had survival value for our distant ancestors, such as the parabolic orbits of flying rocks (explaining our penchant for baseball). A cavewoman thinking too hard about what matter is ultimately made of might fail to notice the tiger sneaking up behind and get cleaned right out of the gene pool. Darwin’s theory thus makes the testable prediction that whenever we use technology to glimpse reality beyond the human scale, our evolved intuition should break down. We’ve repeatedly tested this prediction, and the results overwhelmingly support Darwin. At high speeds, Einstein realized that time slows down, and curmudgeons on the Swedish Nobel committee found this so weird that they refused to give him the Nobel Prize for his relativity theory. At low temperatures, liquid helium can flow upward. At high temperatures, colliding particles change identity; to me, an electron colliding with a positron and turning into a Z-boson feels about as intuitive as two colliding cars turning into a cruise ship. On microscopic scales, particles schizophrenically appear in two places at once, leading to the quantum conundrums mentioned above. On astronomically large scales… weirdness strikes again: if you intuitively understand all aspects of black holes [then you] should immediately put down this book and publish your findings before someone scoops you on the Nobel Prize for quantum gravity… [also,] the leading theory for what happened [in the early universe] suggests that space isn’t merely really really big, but actually infinite, containing infinitely many exact copies of you, and even more near-copies living out every possible variant of your life in two different types of parallel universes.

Like much of modern physics, the hypotheses motivating MIRI’s work can easily run afoul of a reader’s own absurdity heuristic. What are your best tips for getting someone to give up the absurdity heuristic, and try to judge hypotheses via argument and evidence instead?

Max Tegmark: That’s a very important question: I think of the absurdity heuristic as a cognitive bias that’s not only devastating for any scientist hoping to make fundamental discoveries, but also dangerous for any sentient species hoping to avoid extinction. Although it appears daunting to get most people to drop this bias altogether, I think it’s easier if we focus on a specific example. For instance, whereas our instinctive fear of snakes is innate and evolved, our instinctive fear of guns (which the Incas lacked) is learned. Just as people learned to fear nuclear weapons through blockbuster horror movies such as “The Day After”, rational fear of unfriendly AI could undoubtedly be learned through a future horror movie that’s less unrealistic than Terminator III, backed up by a steady barrage of rational arguments from organizations such as MIRI.

In the mean time, I think a good strategy is to confront people with some incontrovertible fact that violates their absurdity heuristic and the whole notion that we’re devoting adequate resources and attention to existential risks. For example, I like to ask why more people have heard of Justin Bieber than of Vasili Arkhipov, even though it wasn’t Justin who singlehandedly prevented a Soviet nuclear attack during the Cuban Missile Crisis.

Luke: After reviewing mainstream contemporary physics, you begin to explain the “multiverse heirarchy” in chapter 6, which refers to four “levels” of multiverse we might inhabit. The “Level I multiverse,” as you call it, is an inescapable prediction of what is currently the most widely accepted theory of the early universe (eternal inflation): the universe is infinite in all directions, implying that there is an identical copy of me, who is also asking Max Tegmark questions via email, roughly 10¹⁰²⁹ meters from where I sit now.

• Infinite space and matter: Early on, there was an infinite space filled with hot expanding plasma.
• Random seeds: Early on, a mechanism operated such that any region could receive any possible seed fluctuations, seemingly at random.

And as you explain, we have pretty decent evidence for these two claims, independent of whether eternal inflation in particular happens to be correct.

Still, I’m curious what your colleagues in physics departments around the world think of this. If you had to guess, what proportion of them accept that the Level I multiverse is a straightforward prediction of eternal inflation? And roughly what proportion of them think eternal inflation, or some theory that assumes both “infinite space and matter” and also “random seeds”, will turn out to be correct?

Max: There’s definitely been an increased acceptance of these ideas, with the most vocal critics shifting from saying “this makes no sense and I hate it!” to “I hate it!”, tacitly acknowleding that it’s actually a scientifically legitimate possibility.

I haven’t seen any relevant poll, but my sense is that the proportion of physicists who think a Level I multiverse is likely depends strongly on their subfield of physics, with the proportion being highest among theoretical cosmologists and high-energy theorists, and lowest in very different areas where people don’t normally think much about these ideas and often feel that they sound too weird to be true.

You and your MIRI colleagues work very hard to be rational, so if you’re convinced that A implies B and A is true, then you’ll update your Bayesian prior to be convinced that B is also true. I suspect that many physicists are less rational than you: my guess is that many who are sympathetic toward inflation and learn that it generically implies eternal inflation and Level I don’t actually update their prior about Level I, but instead tell themselves that a multiverse feels unscientific, and therefore lose interest in spending more time thinking about consequences of inflation.

Luke: You go on to explain four levels of multiverse in total:

• Level I multiverse: “Distant regions of space that are currently but not forever unobservable; they have the same effective laws of physics but may have different histories.” A straightforward prediction of eternal inflation, and many other possible theories of cosmological evolution.
• Level II multiverse: “Distant regions of space that are forever unobservable because space between here and there keeps in inflating; they obey the same fundamental laws of physics, but their effective laws of physics may differ.” Also suggested by eternal inflation.
• Level III multiverse: “Different parts of quantum Hilbert space.” If the wavefunction never collapses but is instead always governed by the Schrödinger equation, this implies the universe is constantly “splitting” into parallel universes.
• Level IV multiverse: “All mathematical structures, corresponding to different fundamental laws of physics.”
• Before we get to Level IV, I want to ask about a claim you make about Level III.

You write that “fledgling technologies such as quantum cryptography and quantum computing explicitly exploit the Level III multiverse and work only if the wavefunction doesn’t collapse.”

But I assume that collapse theorists don’t think their view will be falsified as soon as the first “true” quantum computer is (uncontroversially) built. What do they argue in response? Why do you think quantum computing can only work if the wavefunction doesn’t collapse?

Max: That’s a good question, because there’s lots of confusion in this area. What’s uncontroversial is that quantum computers will work it there’s no collapse, i.e., if the Schrödinger equation works with no exceptions (as long as engineering obstacles such as decoherence mitigation can be overcome). What’s controversial is what happens otherwise. There’s such a large zoo of non-Everett interpretations (13 by now) that you’ll have to ask their adherents what exactly they predict for quantum computers, for quantum systems containing humans, etc. – in my experience, different people claiming to subscribe to the same interpretation sometimes nonetheless disagree on specific predictions.

The quantum litmus test is to ask them the following question:

Alice is in an isolated lab in a spaceship and measures the spin of an electron that was in a superposition of “up” and “down”. According to Bob, who hasn’t yet observed the spaceship, is Alice’s brain in a superposition of perceiving that she’s measured “up” and that she’s measured “down”?

The Many-Worlds Interpretation says unabiguously “yes”, because that’s what the Schrödinger equation predicts. Some Copenhagen supporters would say “no”, on the grounds that Alice collapsed the wavefunction when she observed the electron: something truly random happened at that instant, and it’s now really just up or really just down. Others say “yes” and still others will give you less clear-cut answers. My point is that a theory refusing to make a clear prediction for whether the Schrödinger holds for arbitrary large and complicated systems is automatically refusing to make a prediction for whether an arbitrarily large and complicated quantum computers work or not, and is therefore not a complete theory. I’d also argue that any theory where the wavefunction never collapses is simply Everett disguised in unfamiliar language – as far as nature is concerned, it’s only the equations that matter.

Luke: In chapter 11 you write that:

Whereas most of my physics colleagues would say that our external physical reality is (at least approximately) described by mathematics, I’m arguing that it is mathematics (more specifically, a mathematical structure). In other words, I’m making a much stronger claim. Why? …If a future physics textbook contains the coveted Theory of Everything (ToE), then its equations are a complete description of the mathematical structure that is the external physical reality. I’m writing is rather than corresponds to here, because if two structures are equivalent, then there’s no meaningful sense in which they’re not one and the same…

Do you have physics colleagues who assume external reality exists and that it can be described by mathematics, but who don’t accept your Mathematical Universe Hypothesis? If so, what are their counter-arguments?

Max: Interestingly, I haven’t heard any clearly articulated counter-arguments from physics colleagues. Rather, it’s a bit like with the unfriendly AI X-risk  argument: the scientists I know who are unconvinced by the conclusion don’t take issue with specific logical steps in the argument, but lack sufficient interest in the question to have familiarized themselves with the argument.
If you want to classify people’s views, it boils down to two logically separate questions:

1. Is our external physical reality completely described by mathematics?
2. Can something be perfectly described by mathematics (having no properties except mathematical properties) but still not be a mathematical structure?

The people I’ve heard answer “no” to 1) tend to do so not based on evidence or a logical argument, but based on a preference for a non-mathematical free will, soul or deity. The people I’ve heard answer “no” to 2) often conflate the description with the described, within mathematics itself. This ties in with the important question about whether mathematics is invented or discovered – a famous controversy among mathematicians and philosophers.

Our language for describing the planet Neptune (which we obviously invent – we invented a different word for it in Swedish) is of course distinct from the planet itself, which we discovered. Analogously, we humans invent the language of mathematics (the symbols, our human names for the symbols, etc.), but it’s important not to confuse this language with the structures of mathematics that I focus on in the book. For example, any civilization interested in Platonic solids would discover that there are precisely 5 such structures (the tetrahedron, cube, octahedron, dodecahedron and icosahedron). Whereas they’re free to invent whatever names they want for them, they’re not free to invent a 6th one – it simply doesn’t exist. It’s in the same sense that the mathematical structures that are popular in modern physics are discovered rather than invented, from 3+1-dimensional pseudo-Riemannian manifolds to Hilbert spaces. The possibility that I explore in the book is that one of the structures of mathematics (which we can discover but not invent) corresponds to the physical world (which we also discover rather than invent).

Luke: In chapter 13 you turn your attention to the future of physics, and the future of humanity within the physical world. In particular, you talk a lot about risks of human extinction, aka “existential risks.”

To summarize: the bad news is that there are lots of ways for humans to go extinct. The good news is that very few extinction risks are remotely likely in the next, say, 150 years. To illustrate this point, you provide this graphic:

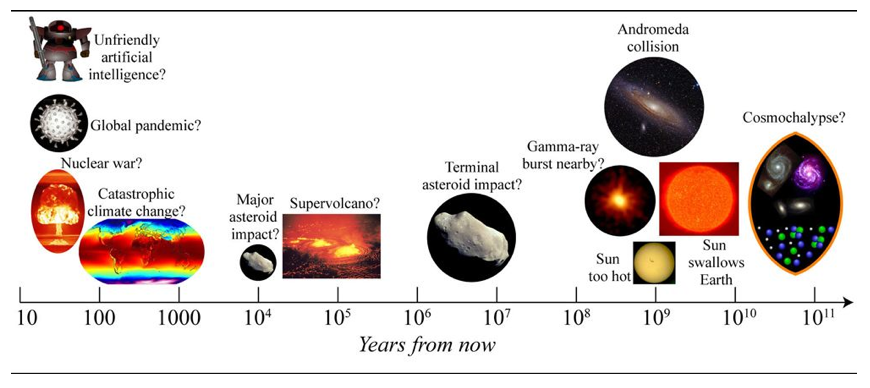
I like that graphic, and I think it’s basically right, except that:

• I’d downplay nuclear war as a fully existential risk (see here),
• I’d change “global pandemic” to “synthetic biology” to emphasize that it’s novel pathogens that might be capable of full-blown human extinction (rather than “mere” global catastrophe),
• and I’d add molecular nanotechnology as a major existential threat for the next 150 years.

I suspect the folks at Cambridge University’s Centre for the Study of Existential Risk (CSER) would make the same adjustments, as they also seem to be focusing on risks from synthetic biology, molecular nanotechnology, and AGI.

Do you think you’d agree with those adjustments, or is your basic picture somewhat different from mine on those points?

Max: I agree that “synthetic biology” is a better phrase, especially since the global pandemics I had in mind when making that figure were mainly human-made. The forms of molecular nanotechnology that I suspect pose the greatest existential risks are those that transcend the boundaries with synthetic biology or AI (already covered).

I disagree with the argument that we’ve overestimated nuclear war as an existential risk. Of course an all-out nuclear war couldn’t kill all humans instantly by literally blowing us up. However, I find the supposedly reassuring arguments you cite unconvincing, and had a spirited debate about this with one of the authors last year. To qualify something as an existential risk, we don’t need to prove that it will extinguish humanity – we simply need to establish reasonable doubt of the assertion that it can’t.

If the initial blasts disable much of our infrastructure and then nuclear winter lowers the summer temperature by about 20°C (36°F) in most of North America, Europe and Asia (as per Robock) to cause catastrophic crop failures, it’s not hard to imagine scenarios of truly existential proportions. Modern human society is a notoriously complex and hard-to-model system, so the scenarios I’m most concerned about involve complex interplays between multiple effects. For example, infrastructure breakdown might make it difficult to control either starvation-induced pandemics or armed gangs who systematically sweep the planet for food, weapons, etc. with little regard for sustainability. Without any serious attempts to model such complications, I don’t find the cited estimates of available biomass etc. particularly reassuring.

Luke: As Bostrom (2013) notes, humanity seems to be investing much more effort into (e.g.) dung beetle research than we are investing in research on near-term existential risks and how we might mitigate them. From your perspective, what can we do to cause research grantmakers (e.g. the NSF) and researchers (e.g. economists) to direct more of their effort toward research into near-term existential risks, especially the risks from novel technologies like synthetic biology and AGI?

Max: We need to draw more attention to these risks, so that people start thinking of them as real threats rather than science fiction fantasies. Organizations such as MIRI are an invaluable step in this direction.

We should aim to make more opinion leaders understand xrisks and make more people who understand xrisks into opinion leaders.

Luke: Thanks, Max!