 Erik DeBenedictis works for Sandia’s Advanced Device Technologies department. He has been a member of the International Technology Roadmap for Semiconductors since 2005.
Erik DeBenedictis works for Sandia’s Advanced Device Technologies department. He has been a member of the International Technology Roadmap for Semiconductors since 2005.
DeBenedictis has received Ph.D. in computer science from Caltech. As a grad student and post-doc, he worked on the hardware that turned into the first hypercube multiprocessor computer. Later dubbed the “Cosmic Cube,” it ran for more than a decade after he left the university and was copied over and over. It’s considered the ancestor of most of today’s supercomputers.
In the 1980s, then working for Bell Labs in Holmdel, N.J., DeBenedictis was part of a consortium competing for the first Gordon Bell award. The team got the second place award, the first place going to Sandia. During the 1990s, he ran NetAlive, Inc., a company developing information management software for desktops and wireless systems. Starting in 2002, DeBenedictis was one of the project leads on the Red Storm supercomputer.
The opinions expressed by Erik below are his own and not those of Sandia or the US Department of Energy. This document has been released by Sandia as SAND Number 2014-2679P.
Luke Muehlhauser: Some of your work involves reversible computing, which I previously discussed with Mike Frank. Mike’s view seemed to be that there were promising signs that reversible computing would be possible eventually, but progress is not moving quickly due to lack of funding and interested researchers. Is that your view as well? And based on my interview with him, do you seem to have a substantially different impression that Mike does about anything he and I discussed?
Erik DeBenedictis: I agree with Mike, but his discussion of minimum energy in computing due to irreversibility is just part of a larger topic of minimum energy in computing that starts with “Moore’s Law Ending.”
For any reader who has not read Mike Frank’s interview, I’d like to give a quick summary of the relevant points. Mike was interviewed about reversible logic, which is sometimes called reversible computing. If you were a brilliant engineer and could figure out how to make a computer logic gate like AND or OR that dissipated kT joules per logic operation (the meaning of kT is in the next paragraph), you would discover that there is an additional heat production on the order of kT due to the interaction between information and thermodynamics. If you were determined to make even lower power computer gates anyway, you would have to use reversible logic principles. You could use a different universal gate set that would include a new gate such as the TOFFOLI or FREDKIN gate. You could also use regular gates (e. g. AND, OR, NOT) and a “retractile cascade” clocking scheme that reverses the computation after you capture the answer.
For reference on kT: k = 1.38 x 10-23 Joules/Kelvin is Boltzmann’s constant and T is the absolute temperature with T = 300 Kelvin at room temperature. kT is about 4 zeptojoules = 4 x 10-21 Joules. Comparing this number to today’s computers is imprecise because dissipation in today’s computers is primarily attributable to the interconnect wire, which varies in length. An AND or OR gate in a modern computer may dissipate a million times this value.
A great many respected scientists believe that reversible computing is feasible, but challenging. If their views are correct, computation should be possible at “arbitrarily low energy levels” and all theories proposing unavoidable, general limits are incorrect. There are a handful of contrary theories proposing minimum energy dissipation levels for computation. Several key ones are Landauer’s Limit of “on the order of kT” per logic operation ((Note added in review: Landauer proposed a lower limit on “on the order of kT” only for “irreversible” computations. As far as I know, the phrase “Landauer’s Limit” was created later by other people. In my experience, the phrase “Landauer’s Limit” if often applied as a general limit.)), a thermal limit of 40-100 kT (depending on your definition of reliable), and the concept in the popular press today that “Moore’s Law is Ending” and the minimum energy per computation is whatever is in the rightmost column of the International Technology Roadmap for Semiconductors (ITRS). That value is about 50,000 kT with typical lengths of interconnect wire.
Scientific situations with multiple competing theories can be settled by a scientific experiment. For example, there is a researcher in New York that has a superconducting circuit running in the sub-kT range and looks like it could demonstrate a logic circuit in another couple “spins” of his chip. Demonstrating and rigorously measuring a sub-kT circuit would invalidate all current theories claiming unavoidable limits.
Whether anybody will fund such an experiment should depend on whether anybody cares about the result, and I’d like to present two society-level questions that the experiment would resolve:
The computer industry started its upward trend during WWII, growing industry revenue and computer throughput in a fairly clean exponential lasting 70 years. The revenue from semiconductors and downstream industries is around $7 trillion per year right now. If there is a lower energy limit to computing, the shift in growth rate will cause a glitch in the world’s economy. My argument is that proving or disproving theories of computing limits could be accomplished for a very small fraction of $7 trillion per year.
The second has to do with profoundly important computational problems, such as the simulation of the global environment to assess climate change issues. Existing climate models running on petaflops supercomputers give varying projections for the future climate, with these projections diverging from observations over the last decade. Regardless of politics, the remedy would be a more sophisticated climate model running on a bigger supercomputer. We don’t know how much bigger, but a zettaflops or more has been mentioned in this context. If any of the minimum energy dissipation theories are correct, the energy dissipation of the required supercomputer could turn out to be too large and climate modeling may be infeasible; if the theory that computing is possible at “arbitrarily low levels” is true, accurate climate modeling will just require a highly-advanced computer.
I’ve tried to expand on Mike’s point: Research on reversible computing could shed light on the future of the economy and the planet’s climate, but I do not know of a single person funded for reversible computing research. Furthermore, a conclusive demonstration of reversible computing would show that there is plenty of room for improving computer efficiency and hence performance. If “Moore’s Law is Ending” means an end to improving computer efficiency, validating reversible computing would show this to be a matter of choice not technology.
Luke: From your perspective, what are the major currently-foreseeable barriers that Moore’s law might crash into before hitting the Landauer limit? (Here, I’m thinking more about the economically important “computations per dollar” formulations of Moore’s law rather than the “serial speed” formulation, which hit a wall in 2004.)
Erik: There is huge upside, but not necessarily for every application. The “computations per dollar” link in the question focused on the use of computers as a platform for strong Artificial Intelligence (AI), so I will comment specifically on that application: I wouldn’t be surprised to see AI accelerated by technology specifically for learning, like neural networks with specialized devices for the equivalent of synapses.
Let’s consider (a) Moore’s Law 1965 to say 2020 and (b) Beyond Moore’s Law 2020+.
From 1965 to 2020, the strategy was to shrink line width. That strategy will be good for 1012 or so increase in computations per dollar.
I see the following classes of advances beyond 2020 that will each give maybe 10-100x efficiency increase each:
- More efficient implementation of the von Neumann architecture.
- More parallelism, with a commensurate increase in the difficulty of programming.
- Software improvements for more efficient execution (e. g. new computer languages and compilers to run general code on Graphics Processing Units).
- Better algorithms that solve a given problem with fewer computations.
- Accelerators, such as CPU+GPU today, extendable to CPU+GPU+various new accelerator types.
- Even at constant energy per gate operation, continued scaling in 2D and better use of the third dimension for reducing communications energy.
- Optical interconnect has upside, but optics is often oversold.
- Nanodevices with behavior different from a transistor that allow some computer functions to be done more efficiently. Examples: Memristors, analog components.
- Improved gate technology through adiabatic methods, sub-threshold or low-threshold operation, or probabilistic computing. Eventually, reversible computing (note below on this one).
- Alternative models of computation (i.e. neuromorphic) that do not use gates as normally defined.
If the ten items in the list above yield an average of 1½ orders of magnitude increase in computations per dollar each, you have more upside than the entire run of Moore’s Law.
If a couple of the items in the list don’t pan out, you could achieve excellent results by concentrating on other paths. So I do not see a general technology crash anytime soon. However, certain specific applications may be dependent on a just a subset of the list above (climate modeling was mentioned) and could be vulnerable to a limit.
Reversible computing plus continued reduction in manufacturing cost per device could extend upside potential tremendously.
However, the necessary technology investment will be greater in the future for a less clear purpose. The message of Moore’s Law was very concise: industry and government invest in line width shrinkage and get a large payoff. In the future, many technology investments will be needed whose purposes have less clear messages.
Bottom line: In general, the path ahead is expensive but will yield a large increase in computations per dollar. Specific application classes could see limits, but they will have to be analyzed specifically.
Luke: What’s your opinion on whether, in the next 15 years, the dark silicon problem will threaten Moore’s Law (computations per dollar)?
Erik: I believe the dark silicon problem will negatively impact computations per dollar. The problem and the underlying energy efficiency problem are going to get worse at least until the cost of increased energy is greater than the cost of refining a solution and bringing it to production. That will happen eventually, but I believe the problem will persist longer than may be expected due momentum against change. However, you admit Moore’s Law has ended when you admit that there is a dark silicon problem.
The underlying cause of dark silicon is that technology scales device dimensions faster than it reduces power. This causes power per unit chip area to increase, which contradicts the key statement in Gordon Moore’s 1965 paper that defined Moore’s Law: “In fact, shrinking dimensions on an integrated structure makes it possible to operate the structure at higher speed for the same power per unit area.”
The mismatched scaling rates create a problem for computations per dollar. Today, the cost of buying a computer is approximately equal to the cost of supplying it with power over its lifetime. Unless power efficiency can be increased, improvements to computer logic will not benefit the user because the amount of computation they use will be limited by the power bill.
The mismatched scaling rates can be accommodated (but not solved) by turning off transistors (dark silicon), packing microprocessors with low energy-density functions like memory (a good idea, to a point), and specialization (described in your interview under dark silicon problem).
The scaling rates could be brought together by more power-efficient transistors, such as the Tunnel Field Effect Transistor (TFET). However, this transistor type will only last a few generations. See here.
Theory says energy per computation can be made “arbitrarily small,” but R&D to exploit these issues will be expensive and disruptive. The leading approaches I am aware of are:
Adiabatic. A fundamentally different approach to logic gate circuits. Example: Mike Frank’s 2LAL.
Certain low-voltage logic classes: For example, see CMOS LP in arXiv 1302.0244 (which is not same as ITRS CMOS LP).
Reversible computing, the topic of Mike Frank’s interview.
The approaches above are disruptive, which I believe limits their popularity today. The approaches use different circuits from CMOS, which would require new design tools. New design tools would be costly to develop and would require retraining of the engineers that use them. Children learn the words “and” and “or” when they are about one year old, with these words becoming the basis of AND and OR in the universal logic basis of computers. To exploit some technologies that save computer power, you have to think in terms of a different logic basis like TOFFOLI, CNOT, and NOT. Some of the ideas above would require people to give up concepts that they learned as infants and have not had reason to question before.
Luke: What do you mean by “you admit Moore’s Law has ended when you admit that there is a dark silicon problem”? The computations-per-dollar Moore’s Law has held up at least through early 2011 (I haven’t checked the data after that), but we’ve known about the dark silicon problem since 2010 or earlier.
Erik: Moore’s Law has had multiple meanings over time, and is also part of a larger activity.
There was a very interesting study by Nordhaus that revealed the peak computation speed of large computers experienced an inflection point around WW II and has been on an upwards exponential ever since. Eyeballing figure 2 of his paper, I’d say the exponential trend started in 1935.
Gordon Moore published a paper in 1965 with the title “Cramming more Components onto Integrated Circuits” that includes a graph of components per chip versus year. As I mentioned for a previous question, the text of the paper includes the sentence, “In fact, shrinking dimensions on an integrated structure makes it possible to operate the structure at higher speed for the same power per unit area.” The graph and previous sentence seem to me to be a subjective description of an underlying scaling rule that was formalized by Dennard in 1974 and is called Dennard scaling.
I have sketched below Moore’s graph of components as a function of year with Nordhaus’ speed as a function of year on the same axes (a reader should be able to obtain the original documents from the links above, which are more compelling than my sketch). This exercise reveals two things: (1) the one-year doubling period in Moore’s paper was too fast, and is now known to be about 18 months, and (2) that Moore’s Law is a subtrend of the growth in computers documented by Nordhaus.
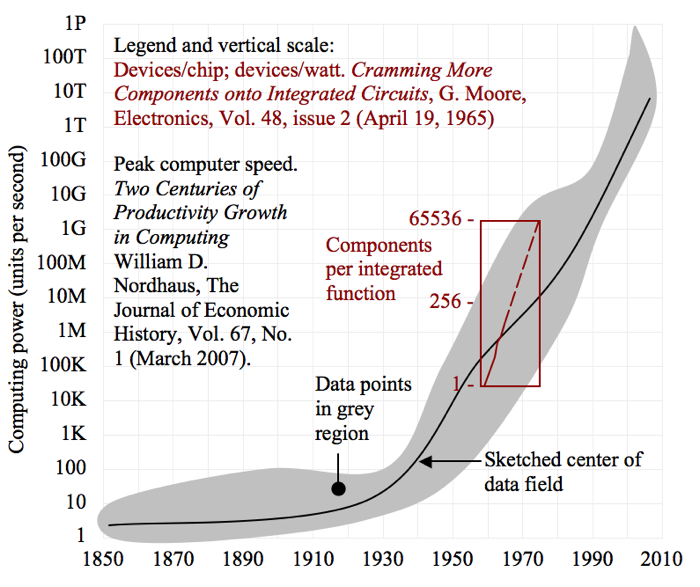
A really interesting question is whether Moore was applying somebody else’s law or whether the two laws were actually part of a larger concept that was not understood at the time. I conclude the latter. Intel did not invent the microprocessor until six years after Moore’s article. I have also talked to people (not Moore) who tell me Gordon Moore was thinking about general electrical circuits and was not foreseeing the emergence of the microprocessor.
Let me try to apply Moore’s Law as defined by his paper. I recall building a computer system in 1981 with an 8086 (very similar to the 8088 in the original IBM PC). I’d heard it was highly complex and dissipated a lot of heat, so I put my finger on it to experience the heat. I recall surprise that it didn’t seem warmer than anything else. I have thought about the heat from microprocessors in the last year, 33 years later. Since Moore’s Law says power per unit area is the same and chips are nearly the same size at 1 cm2, I should be able to put my finger on a chip and not feel any heat. The reality is that there is a new structure sitting on top of today’s microprocessors that reminds me of Darth Vader’s head and is called a “heat sink.” The heat sink is to remove 50-200 watts of heat generated by the chip. I believe I’ve just made a case that any microprocessor with a heat sink violates Moore’s Law.
What’s going on? Moore’s Law is being given additional meaning over and above what Moore was thinking. Many people believe Moore’s Law is only about dimensional scaling, a conclusion supported by the title of his article and the main graph. Moore’s Law has also been associated with computations per dollar, but that law had been around for 30 years before Moore’s paper.
I found the interview with Hadi Esmaeilzadeh on Dark Silicon to be on track, yet he uses another interpretation of Moore’s Law – one where Moore’s Law continues, but Dennard scaling ended in the mid-2000s. Yet, I quoted the phrase from Moore’s paper that disclosed the scaling rule that later became known as Dennard scaling.
At a higher level, I believe Moore’s Law has turned into a marketing phrase that is being redefined as needed by the semiconductor industry so it remains true.
So why are computations per dollar rising? For many years, the vendor objective was to make processors that ran word processors and web browsers faster. This trend culminated in the early 2000s with processors like the Pentium IV with a 4 GHz clock and dissipating 200W+. Customers rebelled and industry shifted to multicore. With an n-core microprocessor, the results of running the benchmark on one core could be multiplied by n. This is an example of progress (raising computations per dollar) by item 2 in my response to a previous question (more parallelism, subject to difficulty in programming). Even now, most software does not exploit the multiple cores.
Luke: You write that “Customers rebelled and industry shifted to multicore.” I typically hear a different story about the 2002-2006 era, one that didn’t have much to do with customer rebellion, but instead the realization by industry that the quickest way to keep up the Moorean trend — to which consumers and manufacturers had become accustomed — was to jump to multicore. That’s the story I see in e.g. The Future of Computing Performance by National Academies Press (official summary here). Moreover, the power scaling challenge to Moore’s Law was anticipated many years in advance by the industry, for example in the ITRS reports. Can you clarify what you mean by “customers rebelled”?
Erik: What happens if you take projections of the future to be true and then the projections change? You eventually end up with multiple “truths” about the same thing in the historical record. I accept that the stories you hear are true, but there is another truth based on different projections.
Let us mathematically invert the ITRS roadmap to see how projections of today’s (2014) microprocessor clock rate evolved as industry addressed power scaling and shifted to multicore. I have gone back to earlier editions of the ITRS and accessed edition reports for 2003, 2005, and 2007. In table 4 of the executive summary of each edition, they have a projection of “on chip local clock,” which means microprocessor clock rate. I accessed Pricewatch to get the 2014 clock rate.
| On chip local clock | In year 2013 | In year 2014 | In year 2015 |
| Projection in 2003 ITRS | 22.9 GHzTable 4c | Only odd years reported in this edition | 33.4 GHzTable 4d |
| Projection in 2005 ITRS | 28.4 GHzTable 4d | ||
| Projection in 2007 ITRS | 7.91 GHzTable 4c | ||
| 2014 reality | 4.0 GHz Pricewatch.com |
The most conspicuous issue is that the 2003 and 2005 editions overstated clock rate by about 7x. ITRS accommodated to multicore in 2007 with a new scaling model that we see in retrospect overstates reality by only 2x. Footnote 1 in the 2007 ITRS describes the change. The footnote ends with the following sentence: “This is to reflect recent on-chip frequency slowing trends and anticipated speed-power design tradeoffs to manage a maximum 200 watts/chip affordable power management tradeoff.”
If you believe ITRS is “industry,” industry had been telling customers to expect the benefits of Moore’s Law through rising clock rate. In my view, customers took the lead in saying power per chip should be less than 200 watts even if it meant a more difficult to use parallel programming model. Several years after the multicore became popular, industry changed its projection so customers were to expect the benefits of progress through rising computations per dollar rather than speed. This, of course, led to the rise of battery operated smart phones and tablets with power limits much lower than 200 watts.
By the way, I have not heard the phrase “Moorean trend” before. It seems to capture the idea of progress in computing without being tied to particular technical property. Why don’t you trademark it; it gets zero Google hits.
Luke: Are you willing to make some forecasts about the next ~15 years in computing? I’d be curious to hear your point estimate, or even better your 70% confidence interval, for any of the following:
- FLOPS per US dollar in top-end supercomputing in 2030.
- Average kT per active logic gate in top-end supercomputing in 2030.
- Some particular measure of progress on reversible computing, in 2030?
- World’s total FLOPS capacity in 2030. (See here.)
Or really, anything specific about computing you’d like to forecast for 2030.
Erik: The FLOPS per dollar question will be most interesting, so I’ll leave it for last.
kT/logic op: I see a plateau around 10,000 kT, and will discuss what might come beyond the plateau in the next paragraph.. My guess of 10,000 kT includes interconnect wire, which is significant because today 75-90% of energy is attributable to interconnect wire. Today, we see around 50,000 kT. A reduction in supply voltage to .3v should be good for 10x improvement, but there are other issues. This estimate should be valid in 10 years, but the question asked about 15 years.
I would not be surprised that we see a new approach in the interval 2025-2030 (mentioned below). It will be difficult to predict specifically, but the five-year interval is short and the improvement rate seems to be insensitive to details. So, say there is a 5x additional improvement by 2030.
Cumulative by 2030: 2,000 kT/logic op, including interconnect wire. However, this will be really disappointing. People will expect 10 doublings due to Moore’s Law in the 15-year interval, for an expected improvement of 1024x; I’m predicting 25x.
Reversible computing: I think reversible computing (as strictly defined) will be demonstrated in a few years and principally impact society’s thought processes. The demonstration would be computation at less than 1 kT/logic op, where theory says those levels are unachievable unless reversible computing principles are used. I do not expect reversible computing to be widely used by 2030. The projection of 2,000 kT/logic op in 2030 represents a balance of manufacturing costs and energy costs.
By 2030, reversible computing could be employed in some applications where power is very expensive, such as spacecraft or implantable medical devices.
However, a demonstration of reversible computing could have an important impact on societal thinking. Popular thinking sees some ideas as unlimited for planning purposes and endows those ideas with attention and investment. This applied to California real estate prices (until 2008) and Moore’s Law (until a few years ago). Claims that “Moore’s Law is Ending” are moving computation into a second class of ideas that popular thinking sees as limited, like the future growth potential of railroads. A reversible computing demonstration would move computing back to the first category and thus make more attention and capital available.
However, reversible computing is part of a continuum. I see a good possibility that adiabatic methods could become the new method mentioned above for the 2020-2025 time range.
World’s Total FLOPS capacity, 2030. I looked over the document by Naik you cited. I don’t feel qualified to judge his result. However, I will stand by my ratio of 50,000 kT to 2,000 kT = 25. So my answer is to multiply Naik’s result by 25. I do not imagine that the cumulative power consumption of computers will rise substantially, particularly with Green initiatives.
FLOPS per dollar: This answer will be all over the place. Let’s break down by application class:
(A) Some applications are CPU-bound, meaning their performance will track changes in kT per logic op. I have given my guess of 25x improvement (which is a lot less then the 1024x that Moore’s Law would have delivered).
(B) Other applications are memory bound, meaning their performance will track (a) memory subsystem performance, where advances partially overlap with advances due to Moore’s Law and (b) architecture changes that can reduce the amount of data movement.
It is a lot easier to make a computer for (A) than (B); for a given cost, a computer will outperform type A applications by an order of magnitude or more on FLOPS compared to type B.
A top-end supercomputer supports both A and B, but the balance between A and B may be the profound question of the era. The balance has been heavily weighted in favor of A (through reliance on LINPACK as the benchmark). However, we do not currently have a particularly aggressive Exascale program in the US. Instead, we have a lot of discussion about the memory subsystem’s low energy efficiency. You can make a fairly compelling case that progress in top-end supercomputing will be held up until the computers can become better balanced.
(For reference the TOP 2 supercomputer is ORNL Titan with 17.5 Petaflops Linpack for $97 million; a ratio of 181 MFLOPS/$. The TOP 1 supercomputer does not seem to be a good cost reference.)
If architecture stays fixed until 2030, I’ll guess 25x improvement. That would be 4.5 GFLOPS/$. Memory subsystems are made out of the same transistor technology as logic, perhaps plus a growing fraction of optics. If transistors become more effective by 25x, this could benefit both FLOPS and the memory subsystem. Use of 3D may boost performance (due to shorter wires), but this will be offset by efficiency loss due to difficulty exploiting greater parallelism. Call the latter factors a wash.
Architecture is the wildcard. There are architectures known that are vastly more efficient than the von Neumann machine, such as systolic arrays, Processor-In-Memory (PIM), Field Programmable Gate Arrays (FPGAs) and even GPUs. These architectures get a performance boost by organizing themselves to put calculations closer to where data is stored, requiring less time and energy to complete a task. Unfortunately, these architectures succeed at the expense of generality. If a vendor boosts performance through too much specialization, they run the risk of being disqualified as an example of a “top-end supercomputer.” The Holy Grail would be a software approach that would make general software run on some specialized hardware (like a compiler that would run general C code on a GPU – at the full performance of the GPU).
However, I will predict that architecture improvements will contribute an additional 4x by 2030, for a cumulative improvement factor of 100x. That will be 18 GFLOPS/$. This is still 10x short of the 1024x expected for 15 years.
However, I think Artificial General Intelligence (AGI) may fare well due to specialization. Synaptic activity is the dominant function that enables living creatures to think, but it is quite different from the floating point in a supercomputer. A synapse performs local, slow, computations based on analog stimuli and analog learned behavior. In contrast, the floating point in a supercomputer operates blazingly fast on data fetched from a distant memory and computes an answer with 64-bit precision. Speed reduces energy efficiency, and the supercomputer doesn’t even learn. Since a von Neumann computer is Turing complete, it will be capable of executing an AGI coded in software. However, the efficiency may be low.
Executing an AGI could be optimized by new or specialized technology and advance faster than the rate of Moore’s Law, like Bitcoin mining. I am going to project that an AGI demonstration at scale will require a non-conventional, but not unimaginable computer. The computer could be specialized CMOS, like a GPU with special data types and data layout. Alternatively, the computer could employ new physical devices, such as a neuromorphic architecture with a non-transistor device (e. g. memristor).
All said, AGI might see 1000x or more improvement. In other words, AGI enthusiasts might be able to plan on 181 GFLOPS/$ by 2030. However, they would be classed as AI machines rather than top-end supercomputers.
Luke: Thanks, Erik!