Dr. Johann Schumann is a member of the Robust Software Engineering Group RSE at NASA Ames. He obtained his habilitation degree (2000) from the Technische Universität München, Germany on application of automated theorem provers in Software Engineering. His PhD thesis (1991) was on high-performance parallel theorem provers. Dr. Schumann is engaged in research on software and system health management, verification and validation of advanced air traffic control algorithms and adaptive systems, statistical data analysis of air traffic control systems and UAS incident data, and the generation of reliable code for data analysis and state estimation. Dr. Schumann’s general research interests focus on the application of formal and statistical methods to improve design and reliability of advanced safety- and security-critical software.
He is employed by SGT, Inc. as Chief Scientist Computational Sciences.
Luke Muehlhauser: In Denney et al. (2006), you and your co-authors helpfully explain:
Software certification aims to show that the software in question achieves a certain level of quality, safety, or security. Its result is a certificate, i.e., independently checkable evidence of the properties claimed. Certification approaches vary widely… but the highest degree of confidence is achieved with approaches that are based on formal methods and use logic and theorem proving to construct the certificates.
We have developed a certification approach which… [demonstrates] the safety of aerospace software which has been automatically generated from high-level specifications. Our core idea is to extend the code generator so that it simultaneously generates code and the detailed annotations… that enable a fully automated safety proof. A verification condition generator (VCG) processes the annotated code and produces a set of safety obligations, which are provable if and only if the code is safe. An automated theorem prover (ATP) then discharges these obligations and the proofs, which can be verified by an independent proof checker, serve as certificates…
…[Our] architecture distinguishes between trusted and untrusted components… Trusted components must be correct because any errors in their results can compromise the assurance given by the system; untrusted components do not affect soundness because their results can be checked by trusted components.
You also include this helpful illustration:
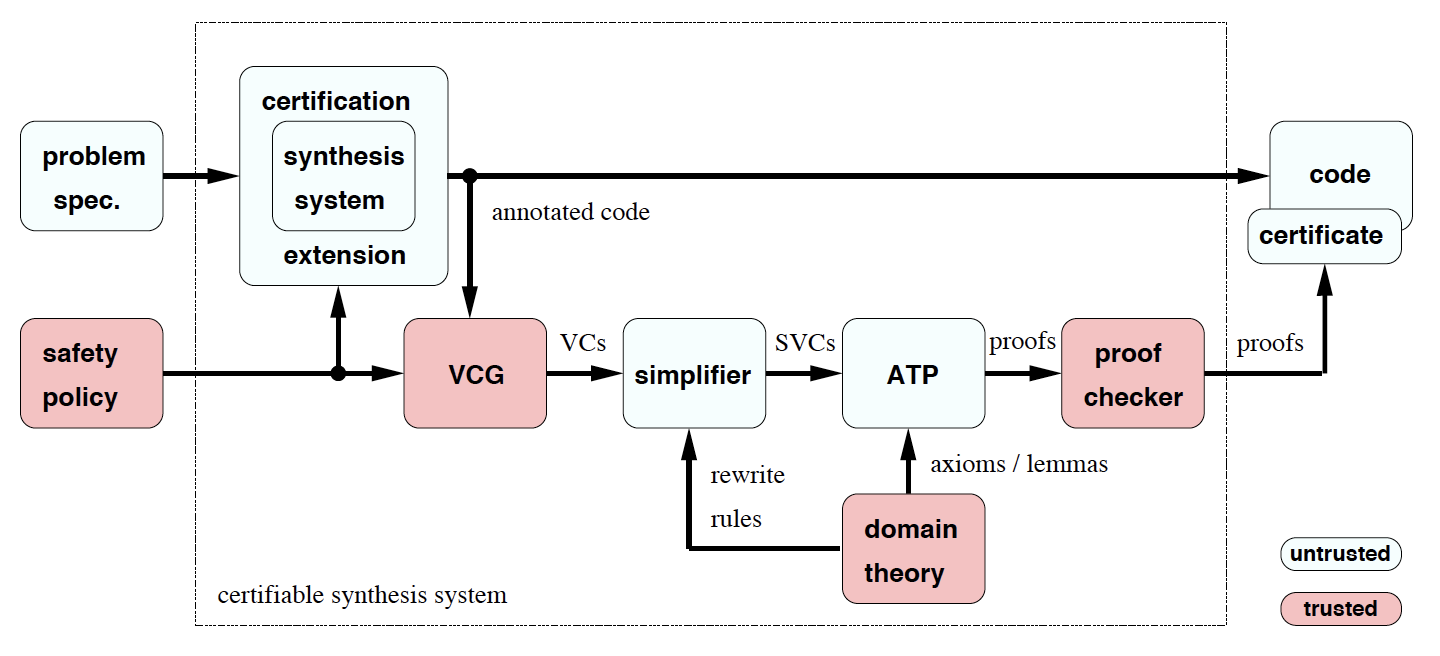
Why are the problem specification and synthesis system untrusted, in your certification system architecture?
Johann Schumann: Ideally, the entire architecture in this figure would only contain trusted components. Then one could be sure that nothing bad happens during the verification process. Unfortunately, software systems like the program synthesis system or an entire automated theorem prover cannot be formally verified with current technology. Their code is tens of thousands of lines of code. We therefore use a trick of problem complexity asymmetry: E.g., a piece of software to find the prime factors of a large number is complex; its verification is complicated and time consuming. On the other hand, checking each individual result is trivial: one just multiplies the factors. Such a checker is easy to implement and to verify. So, if we now use the unverified prime-factor-finder and, for each result, run the quick and small verified checker, we can find out if our prime-factor finder works correctly. Important here is: one needs to run the checker for each result, but since the checker is fast, it doesn’t matter. Similar situation here: synthesis system and prover are large and complicated, but the proof checker isn’t. The VCG is of medium complexity and can be verified. The practical bottleneck of this entire system is that you have to trust your safety policy and the domain theory. Both can be larger set of logic formulas. In my experience: if a formula is longer than 5 lines, it is very likely that it contains a bug. Unfortunately, there is no easy way around that.
Luke: Intuitively, how much “safer” do you think a system developed via formal methods (such as your own process) is, compared to a system developed via normal engineering methods and extensive testing? Have there been any empirical tests of such hypotheses, to your knowledge?
Johann: Intuitively, I think that the use of formal methods (FM) for software development and V&V can substantially increase safety. However, there are a number of issues/considerations:
- Using FMs to verify that certain, well understood safety properties are never violated (e.g., no buffer overflow, no divide-by-zero, no uninitialized variables) is extremely beneficial (see recent security problems — a lot of those have to do with such safety properties). Some technologies for that task (e.g., static analysis) have already achieved much in that direction.
- Even assuming the tools are there, one has to ask: can i specify all necessary security properties? Is the specification of the software, against which I do the FMs based verification, correct and consistent? A correct, consistent, and complete specification is extremely hard to write — so for any software of reasonable complexity, I would assume that there are at least as many bugs in the specification as there are in the code.
- In my opinion, FMs should be used together with traditional methods (including testing) and together with dynamic monitoring. As an example, a formal proof of no-buffer-overflow should be able to reduce (but not eliminate) extensive testing. And since testing only can be finite, dynamic monitoring (aka runtime verification (RV) or software health management (SWHM)) should be used to react on unforeseen software behavior (e.g., caused by dormant bugs or operation in an unexpected environment). RV and SWHM themselves are mostly formal-methods based.
I don’t know of any such empirical tests – they would be very hard to carry out in an unbiased way. Work on cost and reliability modeling (e.g., B. Boehm) might give some insight but I would need to look.
Luke: How effectively do you think formal verification methods will eventually be able to handle more complex safety properties, such as collision avoidance for trains, planes and cars, and Asimovian properties (a la Weld & Etzioni) for systems that interact with humans in general?
Johann: There have been a couple of examples, where formal methods have been successfully used for specification and/or development of a complex system. For example, the B method (a tool-supported method related to the Z method) has been used for the automated train control on the Paris Metro (Line 14). Airbus is using formal methods like abstract interpretation (Cousot) for their development of safety-critical aircraft software.
The TCAS system (Traffic Collision Avoidance System) is a international system on commercial aircraft that warns the pilot from danger of an imminent midair collision (less than a minute away). This complex system (the aircraft need to resolve the conflict among themselves using an elaborate communication protocol) has been studied in detail and formal specifications/analyses exist (e.g., Leveson, Heimdahl and others).
In my opinion, formal methods are strong enough to be used to specify/verify complex systems. However, the Ueberlingen accident showed that this system is not fail-safe. Here “system” means: actual hardware/software, the pilots (who got conflicting messages from the TCAS system and the ATC), the airline (which supposedly told the pilots to ignore warnings and fly the most profitable route), and the swiss air traffic control, which was not fully staffed.
To me it seems that the accurate modeling and prediction of human behavior in a mixed control system (where the human operator has all/partial control) is still a big unsolved issue.
A fully automated system (e.g., UAS) might have safely handled this situation, but in general there are several major issues:
- The acceptance problem (would we board a UAS, would we relinguish the wheel of our cars?). Supposedly when BART first introduced driverless trains, they weren’t accepted by the commuters and they had to put drivers back on the trains.
- How to operate safely in a “mixed-mode” environment? E.g., some cars are automatic, some cars are driven manually, or commerical aircraft versus general aviation and UAS systems. Human operators might make a (silly) mistake or react in an unexpected way. The automated system might react unexpectedly too, e.g., because of a software error.
- How to deal with system security? Many systems to increase safety are currently highly vulnerable to malicious attack: E.g., the ADS-B system, which is supposed to replace parts of the aging ATC system uses an unencrypted protocol; UAS aircraft can be spoofed (see CIA UAS captured by Iran); modern cars can be hacked into easily.
Although a lot has happened in the rigorous treament and specification of complex systems, a number of issues needs to be addressed before we even come close to talk about global properties like the laws of robotics.
How to recover a complex system safely after an operator error? Assume a driver in a car with driving assistence systems (e.g., adaptive cruise control, detection of unsafe lane changes). How does the automated system react to the imminent problem without causing the driver to freak out and make more mistakes?
How to recover the system safely after a problem in the system hardware or software? When the engine exploded on the Qantas A380, the pilots received on the order of 400 diagnostic and error messages, which they had to process (luckily they had the time). Some of the messages contradicted each other or would have been dangerous to carry out.
This shows that it is still a big problem to present the operator with concise and correct status information of a complex system.
After the pilots landed the A380, they couldn’t turn of the engines. First sign of machine intelligence “don’t kill me”?
Luke: Thanks, Johann!
Did you like this post? You may enjoy our other Conversations posts, including:
