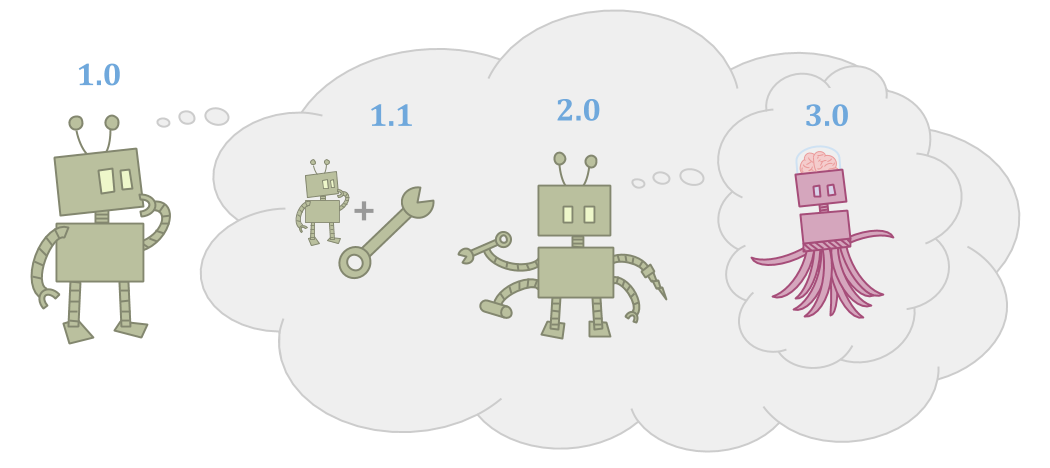
Because the world is big, the agent as it is may be inadequate to accomplish its goals, including in its ability to think.
Because the agent is made of parts, it can improve itself and become more capable.
Improvements can take many forms: The agent can make tools, the agent can make successor agents, or the agent can just learn and grow over time. However, the successors or tools need to be more capable for this to be worthwhile.
This gives rise to a special type of principal/agent problem:
You have an initial agent, and a successor agent. The initial agent gets to decide exactly what the successor agent looks like. The successor agent, however, is much more intelligent and powerful than the initial agent. We want to know how to have the successor agent robustly optimize the initial agent’s goals.
Here are three examples of forms this principal/agent problem can take:
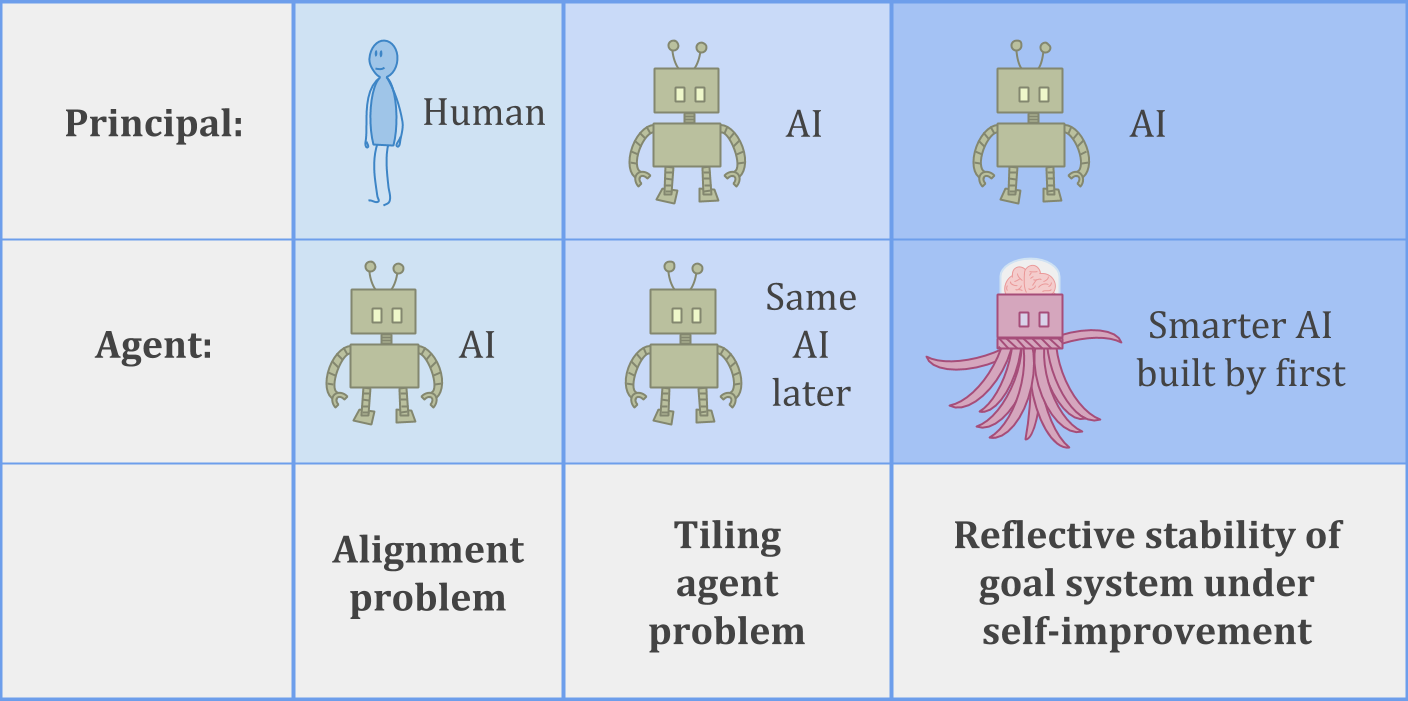
In the AI alignment problem, a human is trying to build an AI system which can be trusted to help with the human’s goals.
In the tiling agents problem, an agent is trying to make sure it can trust its future selves to help with its own goals.
Or we can consider a harder version of the tiling problem—stable self-improvement—where an AI system has to build a successor which is more intelligent than itself, while still being trustworthy and helpful.
For a human analogy which involves no AI, you can think about the problem of succession in royalty, or more generally the problem of setting up organizations to achieve desired goals without losing sight of their purpose over time.
The difficulty seems to be twofold:
First, a human or AI agent may not fully understand itself and its own goals. If an agent can’t write out what it wants in exact detail, that makes it hard for it to guarantee that its successor will robustly help with the goal.
Second, the idea behind delegating work is that you not have to do all the work yourself. You want the successor to be able to act with some degree of autonomy, including learning new things that you don’t know, and wielding new skills and capabilities.
In the limit, a really good formal account of robust delegation should be able to handle arbitrarily capable successors without throwing up any errors—like a human or AI building an unbelievably smart AI, or like an agent that just keeps learning and growing for so many years that it ends up much smarter than its past self.
The problem is not (just) that the successor agent might be malicious. The problem is that we don’t even know what it means not to be.
This problem seems hard from both points of view.
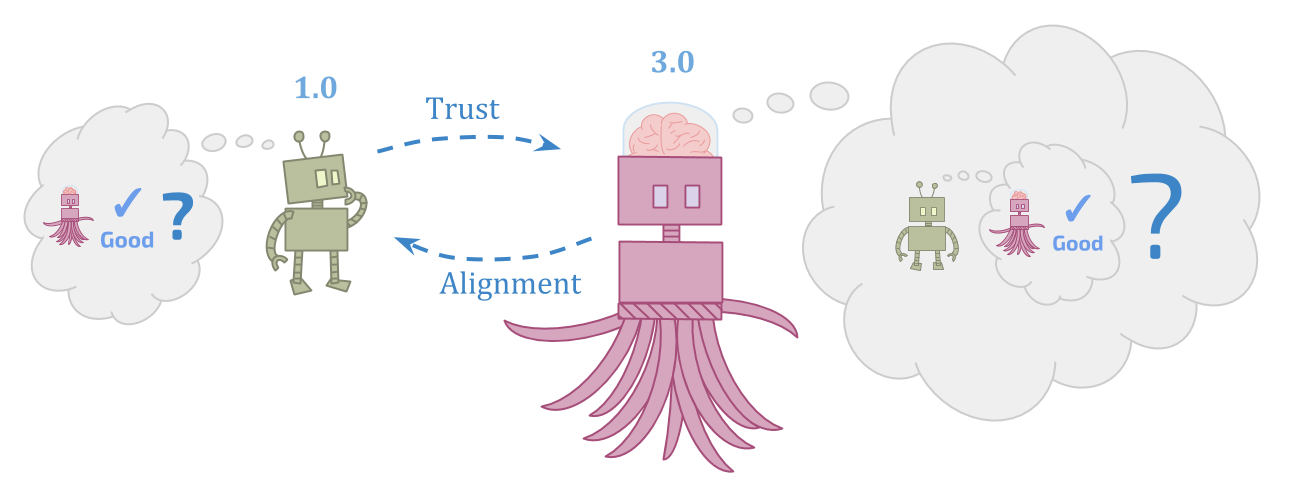
The initial agent needs to figure out how reliable and trustworthy something more powerful than it is, which seems very hard. But the successor agent has to figure out what to do in situations that the initial agent can’t even understand, and try to respect the goals of something that the successor can see is inconsistent, which also seems very hard.
At first, this may look like a less fundamental problem than “make decisions” or “have models”. But the view on which there are multiple forms of the “build a successor” problem is itself a dualistic view.
To an embedded agent, the future self is not privileged; it is just another part of the environment. There isn’t a deep difference between building a successor that shares your goals, and just making sure your own goals stay the same over time.
So, although I talk about “initial” and “successor” agents, remember that this isn’t just about the narrow problem humans currently face of aiming a successor. This is about the fundamental problem of being an agent that persists and learns over time.
We call this cluster of problems Robust Delegation. Examples include:
Imagine you are playing the CIRL game with a toddler.
CIRL means Cooperative Inverse Reinforcement Learning. The idea behind CIRL is to define what it means for a robot to collaborate with a human. The robot tries to pick helpful actions, while simultaneously trying to figure out what the human wants.
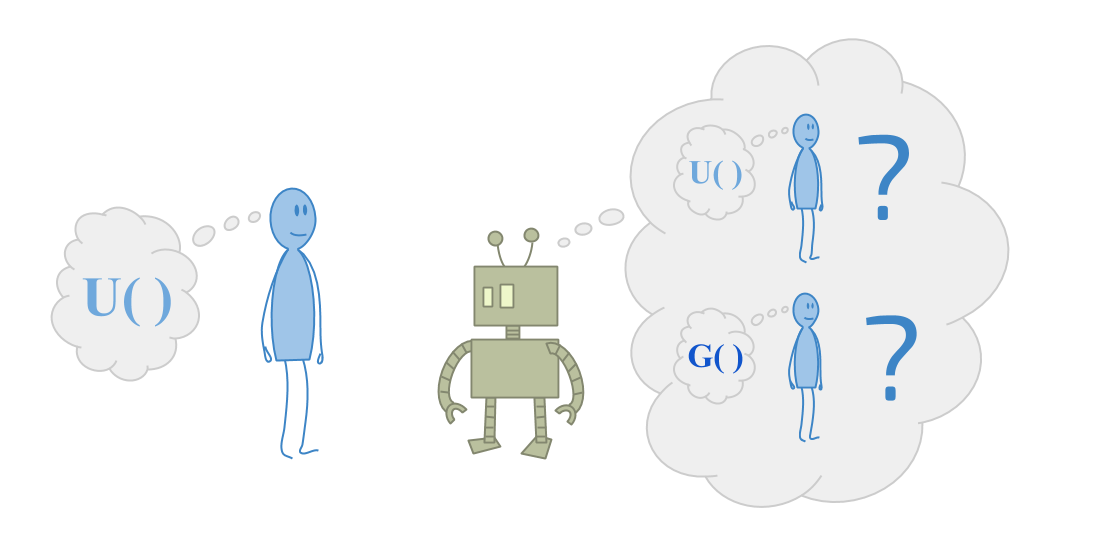
A lot of current work on robust delegation comes from the goal of aligning AI systems with what humans want. So usually, we think about this from the point of view of the human.
But now consider the problem faced by a smart robot, where they’re trying to help someone who is very confused about the universe. Imagine trying to help a toddler optimize their goals.
- From your standpoint, the toddler may be too irrational to be seen as optimizing anything.
- The toddler may have an ontology in which it is optimizing something, but you can see that ontology doesn’t make sense.
- Maybe you notice that if you set up questions in the right way, you can make the toddler seem to want almost anything.
Part of the problem is that the “helping” agent has to be bigger in some sense in order to be more capable; but this seems to imply that the “helped” agent can’t be a very good supervisor for the “helper”.

For example, updateless decision theory eliminates dynamic inconsistencies in decision theory by, rather than maximizing expected utility of your action given what you know, maximizing expected utility of reactions to observations, from a state of ignorance.
Appealing as this may be as a way to achieve reflective consistency, it creates a strange situation in terms of computational complexity: If actions are type \(A\), and observations are type \(O\), reactions to observations are type \(O \to A\)—a much larger space to optimize over than \(A\) alone. And we’re expecting our smaller self to be able to do that!
This seems bad.
One way to more crisply state the problem is: We should be able to trust that our future self is applying its intelligence to the pursuit of our goals without being able to predict precisely what our future self will do. This criterion is called Vingean reflection.
For example, you might plan your driving route before visiting a new city, but you do not plan your steps. You plan to some level of detail, and trust that your future self can figure out the rest.
Vingean reflection is difficult to examine via classical Bayesian decision theory because Bayesian decision theory assumes logical omniscience. Given logical omniscience, the assumption “the agent knows its future actions are rational” is synonymous with the assumption “the agent knows its future self will act according to one particular optimal policy which the agent can predict in advance”.
We have some limited models of Vingean reflection (see “Tiling Agents for Self-Modifying AI, and the Löbian Obstacle” by Yudkowsky and Herreshoff). A successful approach must walk the narrow line between two problems:
- The Löbian Obstacle: Agents who trust their future self because they trust the output of their own reasoning are inconsistent.
- The Procrastination Paradox: Agents who trust their future selves without reason tend to be consistent but unsound and untrustworthy, and will put off tasks forever because they can do them later.
The Vingean reflection results so far apply only to limited sorts of decision procedures, such as satisficers aiming for a threshold of acceptability. So there is plenty of room for improvement, getting tiling results for more useful decision procedures and under weaker assumptions.
However, there is more to the robust delegation problem than just tiling and Vingean reflection.
When you construct another agent, rather than delegating to your future self, you more directly face a problem of value loading.
The main problems here:
- We don’t know what we want.
- Optimization amplifies slight differences between what we say we want and what we really want.
The misspecification-amplifying effect is known as Goodhart’s Law, named for Charles Goodhart’s observation: “Any observed statistical regularity will tend to collapse once pressure is placed upon it for control purposes.”
When we specify a target for optimization, it is reasonable to expect it to be correlated with what we want—highly correlated, in some cases. Unfortunately, however, this does not mean that optimizing it will get us closer to what we want—especially at high levels of optimization.
There are (at least) four types of Goodhart: regressional, extremal, causal, and adversarial.
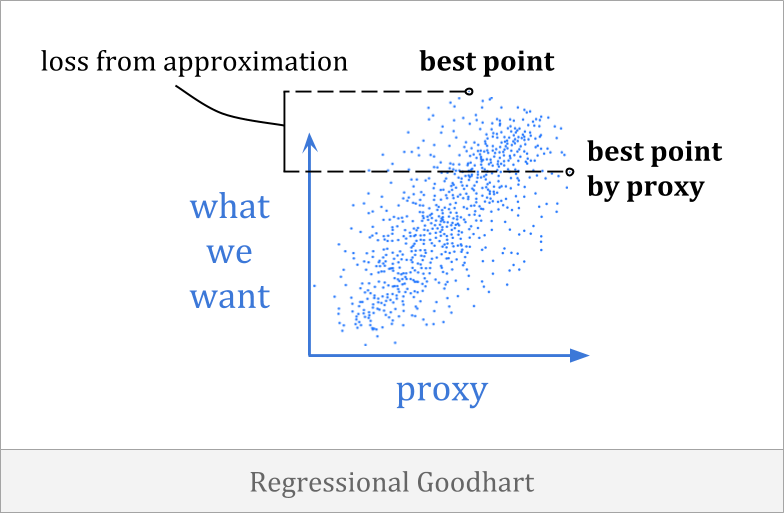
Regressional Goodhart happens when there is a less than perfect correlation between the proxy and the goal. It is more commonly known as the optimizer’s curse, and it is related to regression to the mean.
An example of regressional Goodhart is that you might draft players for a basketball team based on height alone. This isn’t a perfect heuristic, but there is a correlation between height and basketball ability, which you can make use of in making your choices.
It turns out that, in a certain sense, you will be predictably disappointed if you expect the general trend to hold up as strongly for your selected team.
Stated in statistical terms: an unbiased estimate of \(y\) given \(x\) is not an unbiased estimate of \(y\) when we select for the best \(x\). In that sense, we can expect to be disappointed when we use \(x\) as a proxy for \(y\) for optimization purposes.
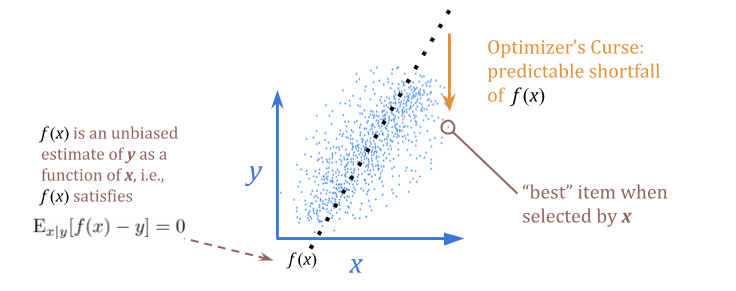
(The graphs in this section are hand-drawn to help illustrate the relevant concepts.)
Using a Bayes estimate instead of an unbiased estimate, we can eliminate this sort of predictable disappointment. The Bayes estimate accounts for the noise in \(x\), bending toward typical \(y\) values.
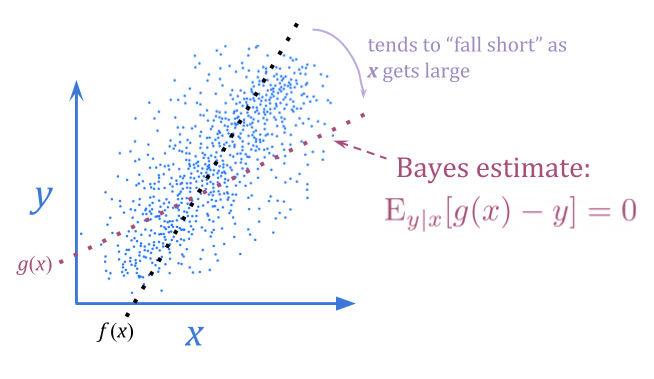
This doesn’t necessarily allow us to get a better \(y\) value, since we still only have the information content of \(x\) to work with. However, it sometimes may. If \(y\) is normally distributed with variance \(1\), and \(x\) is \(y \pm 10\) with even odds of \(+\) or \(-\), a Bayes estimate will give better optimization results by almost entirely removing the noise.
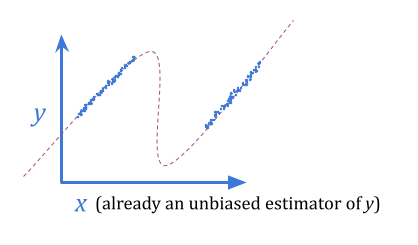
Regressional Goodhart seems like the easiest form of Goodhart to beat: just use Bayes!
However, there are two big problems with this solution:
- Bayesian estimators are very often intractable in cases of interest.
- It only makes sense to trust the Bayes estimate under a realizability assumption.
A case where both of these problems become critical is computational learning theory.
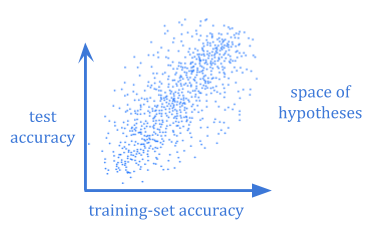
It often isn’t computationally feasible to calculate the Bayesian expected generalization error of a hypothesis. And even if you could, you would still need to wonder whether your chosen prior reflected the world well enough.
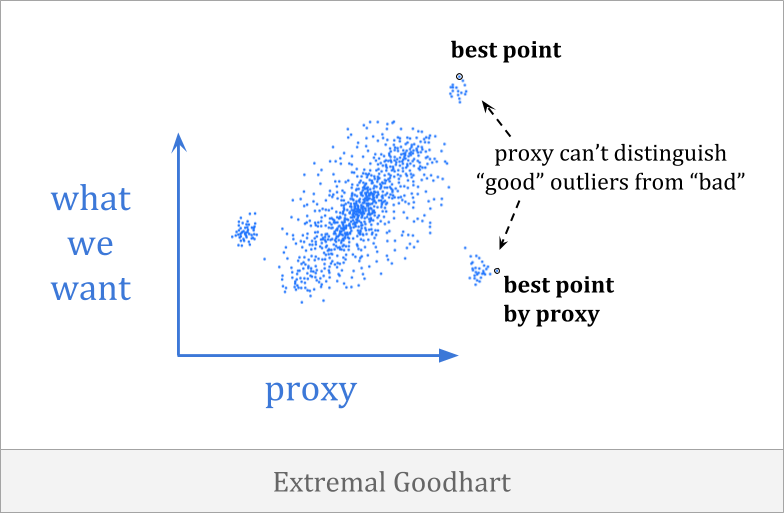
In extremal Goodhart, optimization pushes you outside the range where the correlation exists, into portions of the distribution which behave very differently.
This is especially scary because it tends to involves optimizers behaving in sharply different ways in different contexts, often with little or no warning. You might not be able to observe the proxy breaking down at all when you have weak optimization, but once the optimization becomes strong enough, you can enter a very different domain.
The difference between extremal Goodhart and regressional Goodhart is related to the classical interpolation/extrapolation distinction.
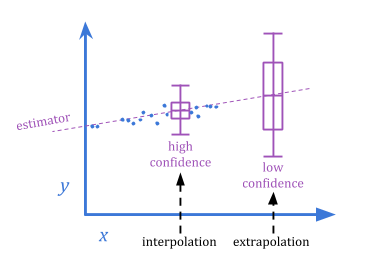
Because extremal Goodhart involves a sharp change in behavior as the system is scaled up, it’s harder to anticipate than regressional Goodhart.
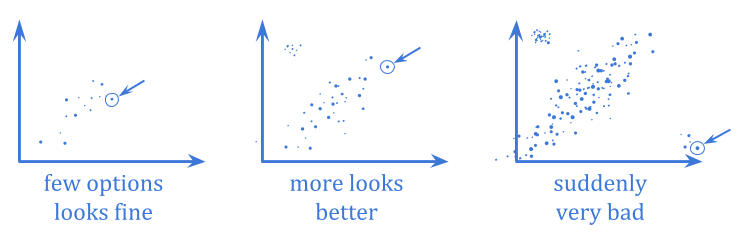
As in the regressional case, a Bayesian solution addresses this concern in principle, if you trust a probability distribution to reflect the possible risks sufficiently well. However, the realizability concern seems even more prominent here.
Can a prior be trusted to anticipate problems with proposals, when those proposals have been highly optimized to look good to that specific prior? Certainly a human’s judgment couldn’t be trusted under such conditions—an observation which suggests that this problem will remain even if a system’s judgments about values perfectly reflect a human’s.
We might say that the problem is this: “typical” outputs avoid extremal Goodhart, but “optimizing too hard” takes you out of the realm of the typical.
But how can we formalize “optimizing too hard” in decision-theoretic terms?
Quantilization offers a formalization of “optimize this some, but don’t optimize too much”.
Imagine a proxy \(V(x)\) as a “corrupted” version of the function we really want, \(U(x)\). There might be different regions where the corruption is better or worse.
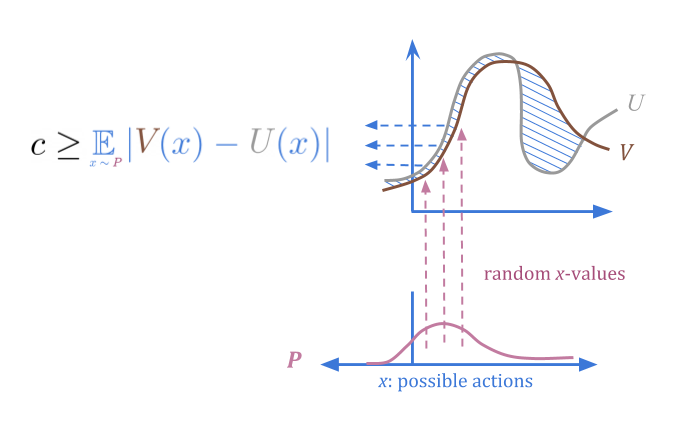
Suppose that we can additionally specify a “trusted” probability distribution \(P(x)\), for which we are confident that the average error is below some threshold \(c\).
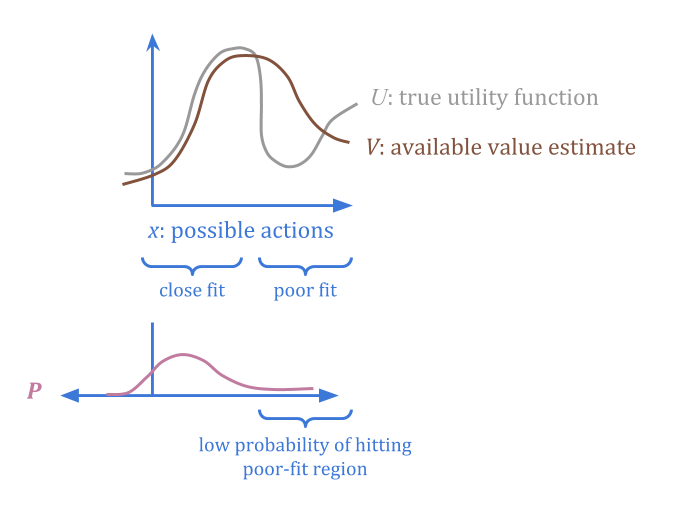
By stipulating \(P\) and \(c\), we give information about where to find low-error points, without needing to have any estimates of \(U\) or of the actual error at any one point.
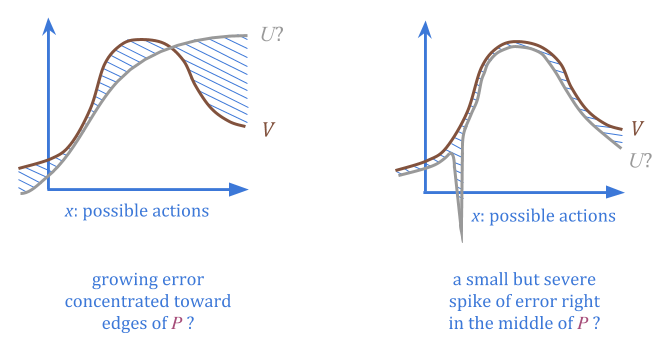
When we select actions from \(P\) at random, we can be sure regardless that there’s a low probability of high error.
So, how do we use this to optimize? A quantilizer selects from \(P\), but discarding all but the top fraction \(f\); for example, the top 1%. In this visualization, I’ve judiciously chosen a fraction that still has most of the probability concentrated on the “typical” options, rather than on outliers:
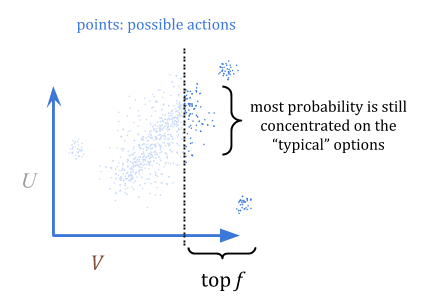
By quantilizing, we can guarantee that if we overestimate how good something is, we’re overestimating by at most \(\frac{c}{f}\) in expectation. This is because in the worst case, all of the overestimation was of the \(f\) best options.
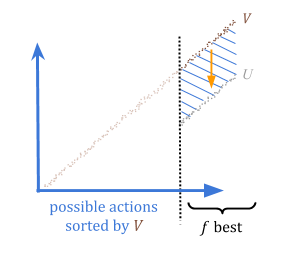
We can therefore choose an acceptable risk level, \(r = \frac{c}{f}\), and set the parameter \(f\) as \(\frac{c}{r}\).
Quantilization is in some ways very appealing, since it allows us to specify safe classes of actions without trusting every individual action in the class—or without trusting any individual action in the class.
If you have a sufficiently large heap of apples, and there’s only one rotten apple in the heap, choosing randomly is still very likely safe. By “optimizing less hard” and picking a random good-enough action, we make the really extreme options low-probability. In contrast, if we had optimized as hard as possible, we might have ended up selecting from only bad apples.
However, this approach also leaves a lot to be desired. Where do “trusted” distributions come from? How do you estimate the expected error \(c\), or select the acceptable risk level \(r\)? Quantilization is a risky approach because \(r\) gives you a knob to turn that will seemingly improve performance, while increasing risk, until (possibly sudden) failure.
Additionally, quantilization doesn’t seem likely to tile. That is, a quantilizing agent has no special reason to preserve the quantilization algorithm when it makes improvements to itself or builds new agents.
So there seems to be room for improvement in how we handle extremal Goodhart.
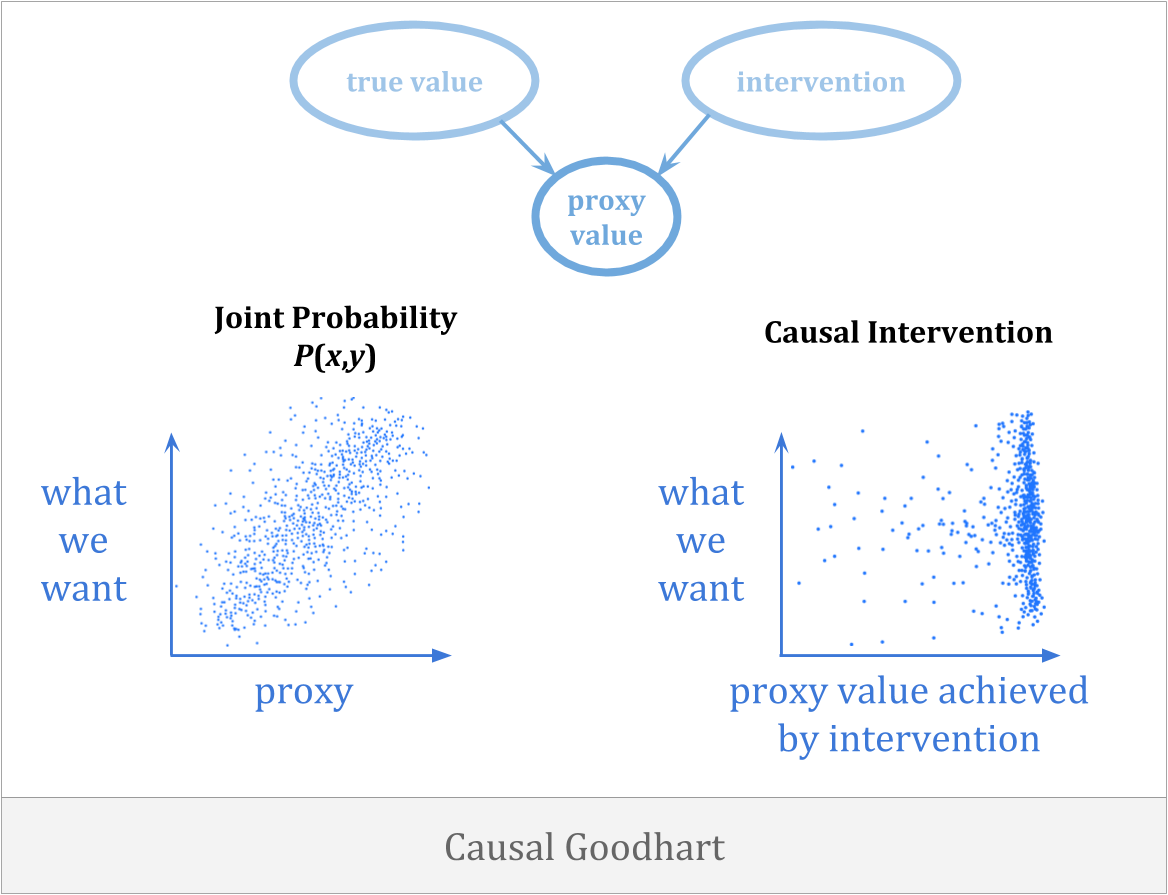
Another way optimization can go wrong is when the act of selecting for a proxy breaks the connection to what we care about. Causal Goodhart happens when you observe a correlation between proxy and goal, but when you intervene to increase the proxy, you fail to increase the goal because the observed correlation was not causal in the right way.
An example of causal Goodhart is that you might try to make it rain by carrying an umbrella around. The only way to avoid this sort of mistake is to get counterfactuals right.
This might seem like punting to decision theory, but the connection here enriches robust delegation and decision theory alike.
Counterfactuals have to address concerns of trust due to tiling concerns—the need for decision-makers to reason about their own future decisions. At the same time, trust has to address counterfactual concerns because of causal Goodhart.
Once again, one of the big challenges here is realizability. As we noted in our discussion of embedded world-models, even if you have the right theory of how counterfactuals work in general, Bayesian learning doesn’t provide much of a guarantee that you’ll learn to select actions well, unless we assume realizability.
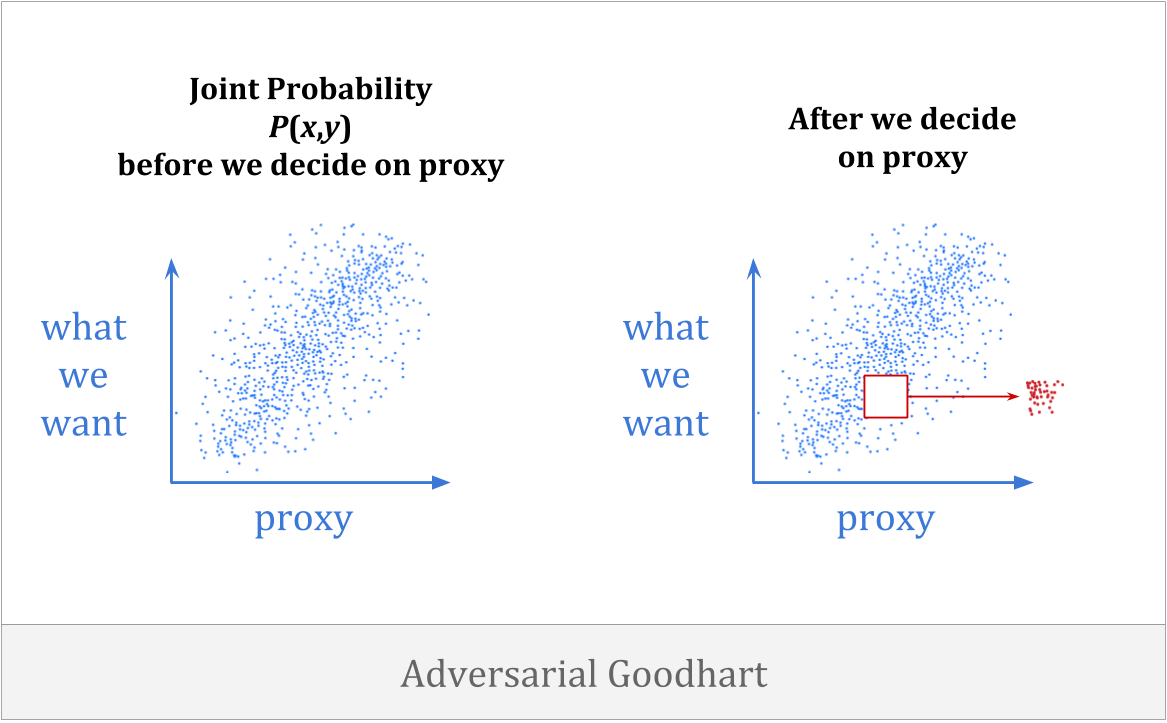
Finally, there is adversarial Goodhart, in which agents actively make our proxy worse by intelligently manipulating it.
This category is what people most often have in mind when they interpret Goodhart’s remark. And at first glance, it may not seem as relevant to our concerns here. We want to understand in formal terms how agents can trust their future selves, or trust helpers they built from scratch. What does that have to do with adversaries?
The short answer is: when searching in a large space which is sufficiently rich, there are bound to be some elements of that space which implement adversarial strategies. Understanding optimization in general requires us to understand how sufficiently smart optimizers can avoid adversarial Goodhart. (We’ll come back to this point in our discussion of subsystem alignment.)
The adversarial variant of Goodhart’s law is even harder to observe at low levels of optimization, both because the adversaries won’t want to start manipulating until after test time is over, and because adversaries that come from the system’s own optimization won’t show up until the optimization is powerful enough.
These four forms of Goodhart’s law work in very different ways—and roughly speaking, they tend to start appearing at successively higher levels of optimization power, beginning with regressional Goodhart and proceeding to causal, then extremal, then adversarial. So be careful not to think you’ve conquered Goodhart’s law because you’ve solved some of them.
Besides anti-Goodhart measures, it would obviously help to be able to specify what we want precisely. Remember that none of these problems would come up if a system were optimizing what we wanted directly, rather than optimizing a proxy.
Unfortunately, this is hard. So can the AI system we’re building help us with this?
More generally, can a successor agent help its predecessor solve this? Maybe it can use its intellectual advantages to figure out what we want?
AIXI learns what to do through a reward signal which it gets from the environment. We can imagine humans have a button which they press when AIXI does something they like.
The problem with this is that AIXI will apply its intelligence to the problem of taking control of the reward button. This is the problem of wireheading.
This kind of behavior is potentially very difficult to anticipate; the system may deceptively behave as intended during training, planning to take control after deployment. This is called a “treacherous turn”.
Maybe we build the reward button into the agent, as a black box which issues rewards based on what is going on. The box could be an intelligent sub-agent in its own right, which figures out what rewards humans would want to give. The box could even defend itself by issuing punishments for actions aimed at modifying the box.
In the end, though, if the agent understands the situation, it will be motivated to take control anyway.
If the agent is told to get high output from “the button” or “the box”, then it will be motivated to hack those things. However, if you run the expected outcomes of plans through the actual reward-issuing box, then plans to hack the box are evaluated by the box itself, which won’t find the idea appealing.
Daniel Dewey calls the second sort of agent an observation-utility maximizer. (Others have included observation-utility agents within a more general notion of reinforcement learning.)
I find it very interesting how you can try all sorts of things to stop an RL agent from wireheading, but the agent keeps working against it. Then, you make the shift to observation-utility agents and the problem vanishes.
However, we still have the problem of specifying \(U\). Daniel Dewey points out that observation-utility agents can still use learning to approximate \(U\) over time; we just can’t treat \(U\) as a black box. An RL agent tries to learn to predict the reward function, whereas an observation-utility agent uses estimated utility functions from a human-specified value-learning prior.
However, it’s still difficult to specify a learning process which doesn’t lead to other problems. For example, if you’re trying to learn what humans want, how do you robustly identify “humans” in the world? Merely statistically decent object recognition could lead back to wireheading.
Even if you successfully solve that problem, the agent might correctly locate value in the human, but might still be motivated to change human values to be easier to satisfy. For example, suppose there is a drug which modifies human preferences to only care about using the drug. An observation-utility agent could be motivated to give humans that drug in order to make its job easier. This is called the human manipulation problem.
Anything marked as the true repository of value gets hacked. Whether this is one of the four types of Goodharting, or a fifth, or something all its own, it seems like a theme.
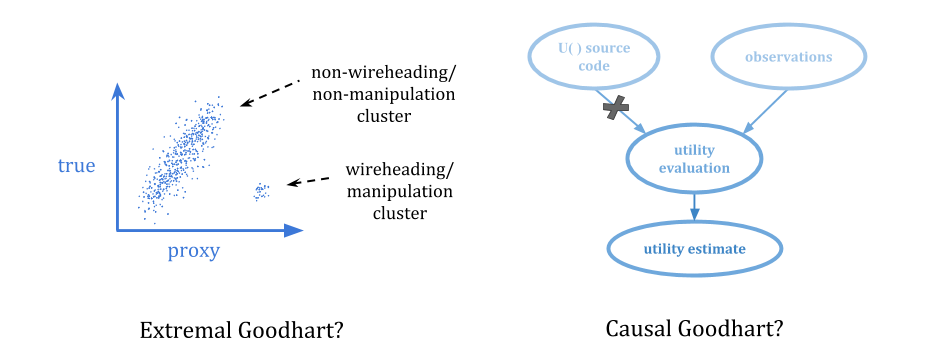
The challenge, then, is to create stable pointers to what we value: an indirect reference to values not directly available to be optimized, which doesn’t thereby encourage hacking the repository of value.
One important point is made by Tom Everitt et al. in “Reinforcement Learning with a Corrupted Reward Channel“: the way you set up the feedback loop makes a huge difference.
They draw the following picture:
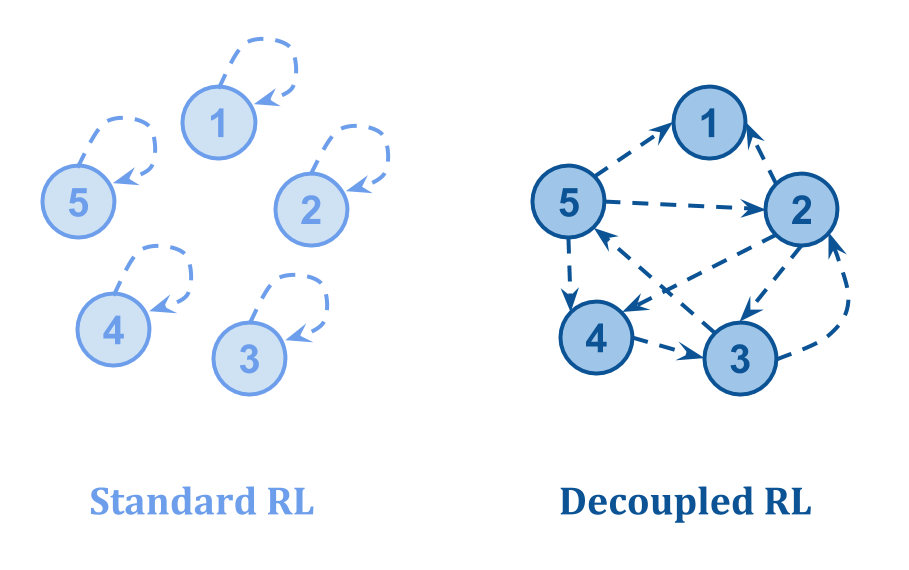
- In Standard RL, the feedback about the value of a state comes from the state itself, so corrupt states can be “self-aggrandizing”.
- In Decoupled RL, the feedback about the quality of a state comes from some other state, making it possible to learn correct values even when some feedback is corrupt.
In some sense, the challenge is to put the original, small agent in the feedback loop in the right way. However, the problems with updateless reasoning mentioned earlier make this hard; the original agent doesn’t know enough.
One way to try to address this is through intelligence amplification: try to turn the original agent into a more capable one with the same values, rather than creating a successor agent from scratch and trying to get value loading right.
For example, Paul Christiano proposes an approach in which the small agent is simulated many times in a large tree, which can perform complex computations by splitting problems into parts.
However, this is still fairly demanding for the small agent: it doesn’t just need to know how to break problems down into more tractable pieces; it also needs to know how to do so without giving rise to malign subcomputations.
For example, since the small agent can use the copies of itself to get a lot of computational power, it could easily try to use a brute-force search for solutions that ends up running afoul of Goodhart’s Law.
This issue is the subject of the next section: subsystem alignment.
This is part of Abram Demski and Scott Garrabrant’s Embedded Agency sequence. Continue to the next part.
Did you like this post? You may enjoy our other Analysis posts, including: