
You want to figure something out, but you don’t know how to do that yet.
You have to somehow break up the task into sub-computations. There is no atomic act of “thinking”; intelligence must be built up of non-intelligent parts.
The agent being made of parts is part of what made counterfactuals hard, since the agent may have to reason about impossible configurations of those parts.
Being made of parts is what makes self-reasoning and self-modification even possible.
What we’re primarily going to discuss in this section, though, is another problem: when the agent is made of parts, there could be adversaries not just in the external environment, but inside the agent as well.
This cluster of problems is Subsystem Alignment: ensuring that subsystems are not working at cross purposes; avoiding subprocesses optimizing for unintended goals.
- benign induction
- benign optimization
- transparency
- mesa-optimizers
Here’s a straw agent design:
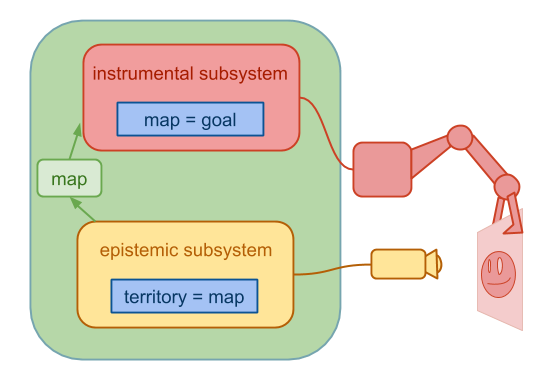
The epistemic subsystem just wants accurate beliefs. The instrumental subsystem uses those beliefs to track how well it is doing. If the instrumental subsystem gets too capable relative to the epistemic subsystem, it may decide to try to fool the epistemic subsystem, as depicted.
If the epistemic subsystem gets too strong, that could also possibly yield bad outcomes.
This agent design treats the system’s epistemic and instrumental subsystems as discrete agents with goals of their own, which is not particularly realistic. However, we saw in the section on wireheading that the problem of subsystems working at cross purposes is hard to avoid. And this is a harder problem if we didn’t intentionally build the relevant subsystems.
One reason to avoid booting up sub-agents who want different things is that we want robustness to relative scale.
An approach is robust to scale if it still works, or fails gracefully, as you scale capabilities. There are three types: robustness to scaling up; robustness to scaling down; and robustness to relative scale.
- Robustness to scaling up means that your system doesn’t stop behaving well if it gets better at optimizing. One way to check this is to think about what would happen if the function the AI optimizes were actually maximized. Think Goodhart’s Law.
- Robustness to scaling down means that your system still works if made less powerful. Of course, it may stop being useful; but it should fail safely and without unnecessary costs.
Your system might work if it can exactly maximize some function, but is it safe if you approximate? For example, maybe a system is safe if it can learn human values very precisely, but approximation makes it increasingly misaligned.
- Robustness to relative scale means that your design does not rely on the agent’s subsystems being similarly powerful. For example, GAN (Generative Adversarial Network) training can fail if one sub-network gets too strong, because there’s no longer any training signal.
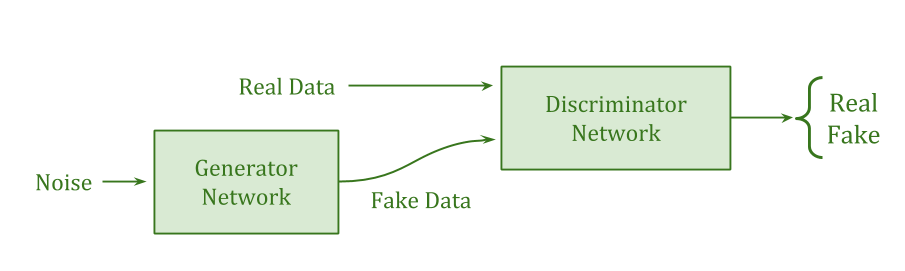
Lack of robustness to scale isn’t necessarily something which kills a proposal, but it is something to be aware of; lacking robustness to scale, you need strong reason to think you’re at the right scale.
Robustness to relative scale is particularly important for subsystem alignment. An agent with intelligent sub-parts should not rely on being able to outsmart them, unless we have a strong account of why this is always possible.
The big-picture moral: aim to have a unified system that doesn’t work at cross purposes to itself.
Why would anyone make an agent with parts fighting against one another? There are three obvious reasons: subgoals, pointers, and search.
Splitting up a task into subgoals may be the only way to efficiently find a solution. However, a subgoal computation shouldn’t completely forget the big picture!
An agent designed to build houses should not boot up a sub-agent who cares only about building stairs.
One intuitive desideratum is that although subsystems need to have their own goals in order to decompose problems into parts, the subgoals need to “point back” robustly to the main goal.
A house-building agent might spin up a subsystem that cares only about stairs, but only cares about stairs in the context of houses.
However, you need to do this in a way that doesn’t just amount to your house-building system having a second house-building system inside its head. This brings me to the next item:
Pointers: It may be difficult for subsystems to carry the whole-system goal around with them, since they need to be reducing the problem. However, this kind of indirection seems to encourage situations in which different subsystems’ incentives are misaligned.
As we saw in the example of the epistemic and instrumental subsystems, as soon as we start optimizing some sort of expectation, rather than directly getting feedback about what we’re doing on the metric that’s actually important, we may create perverse incentives—that’s Goodhart’s Law.
How do we ask a subsystem to “do X” as opposed to “convince the wider system that I’m doing X”, without passing along the entire overarching goal-system?
This is similar to the way we wanted successor agents to robustly point at values, since it is too hard to write values down. However, in this case, learning the values of the larger agent wouldn’t make any sense either; subsystems and subgoals need to be smaller.
It might not be that difficult to solve subsystem alignment for subsystems which humans entirely design, or subgoals which an AI explicitly spins up. If you know how to avoid misalignment by design and robustly delegate your goals, both problems seem solvable.
However, it doesn’t seem possible to design all subsystems so explicitly. At some point, in solving a problem, you’ve split it up as much as you know how to and must rely on some trial and error.
This brings us to the third reason subsystems might be optimizing different things, search: solving a problem by looking through a rich space of possibilities, a space which may itself contain misaligned subsystems.

ML researchers are quite familiar with the phenomenon: it’s easier to write a program which finds a high-performance machine translation system for you than to directly write one yourself.
In the long run, this process can go one step further. For a rich enough problem and an impressive enough search process, the solutions found via search might themselves be intelligently optimizing something.
This might happen by accident, or be purposefully engineered as a strategy for solving difficult problems. Either way, it stands a good chance of exacerbating Goodhart-type problems—you now effectively have two chances for misalignment, where you previously had one.
This problem is described in Hubinger, et al.’s “Risks from Learned Optimization in Advanced Machine Learning Systems”.
Let’s call the original search process the base optimizer, and the search process found via search a mesa-optimizer.
“Mesa” is the opposite of “meta”. Whereas a “meta-optimizer” is an optimizer designed to produce a new optimizer, a “mesa-optimizer” is any optimizer generated by the original optimizer—whether or not the programmers wanted their base optimizer to be searching for new optimizers.
“Optimization” and “search” are ambiguous terms. I’ll think of them as any algorithm which can be naturally interpreted as doing significant computational work to “find” an object that scores highly on some objective function.
The objective function of the base optimizer is not necessarily the same as that of the mesa-optimizer. If the base optimizer wants to make pizza, the new optimizer may enjoy kneading dough, chopping ingredients, et cetera.
The new optimizer’s objective function must be helpful for the base objective, at least in the examples the base optimizer is checking. Otherwise, the mesa-optimizer would not have been selected.
However, the mesa-optimizer must reduce the problem somehow; there is no point to it running the exact same search all over again. So it seems like its objectives will tend to be like good heuristics; easier to optimize, but different from the base objective in general.
Why might a difference between base objectives and mesa-objectives be concerning, if the new optimizer is scoring highly on the base objective anyway? It’s about the interplay with what’s really wanted. Even if we get value specification exactly right, there will always be some distributional shift between the training set and deployment. (See Amodei, et al.’s “Concrete Problems in AI Safety”.)
Distributional shifts which would be small in ordinary cases may make a big difference to a capable mesa-optimizer, which may observe the slight difference and figure out how to capitalize on it for its own objective.
Actually, to even use the term “distributional shift” seems wrong in the context of embedded agency. The world is not i.i.d. The analog of “no distributional shift” would be to have an exact model of the whole future relevant to what you want to optimize, and the ability to run it over and over during training. So we need to deal with massive “distributional shift”.
We may also want to optimize for things that aren’t exactly what we want. The obvious way to avoid agents that pursue subgoals at the cost of the overall goal is to have the subsystems not be agentic. Just search over a bunch of ways to make stairs, don’t make something that cares about stairs.
The problem is then that powerful mesa-optimizers are optimizing something the base system doesn’t care about, and that the mesa-optimizers will have a convergent incentive to be agentic.
Additionally, there’s the possibility that the mesa-optimizer becomes aware of the base optimizer, in which case it might start explicitly trying to do well on the base objective function purely in order to be kept around, while looking for any signs that it has left training and can stop pretending. This creates a version of Nick Bostrom’s “treacherous turn”.
This is the same story we saw in adversarial Goodhart: there is something agentic in the search space, which responds to our choice of proxy in a way which makes our proxy a bad one.
You might try to avoid treacherous turns by repeatedly simulating “end of training, time for deployment” during training, in a kind of nested-dream setup. The goal is to test enough layers of simulation that you can conclude there won’t be a treacherous turn in the real deployment case.
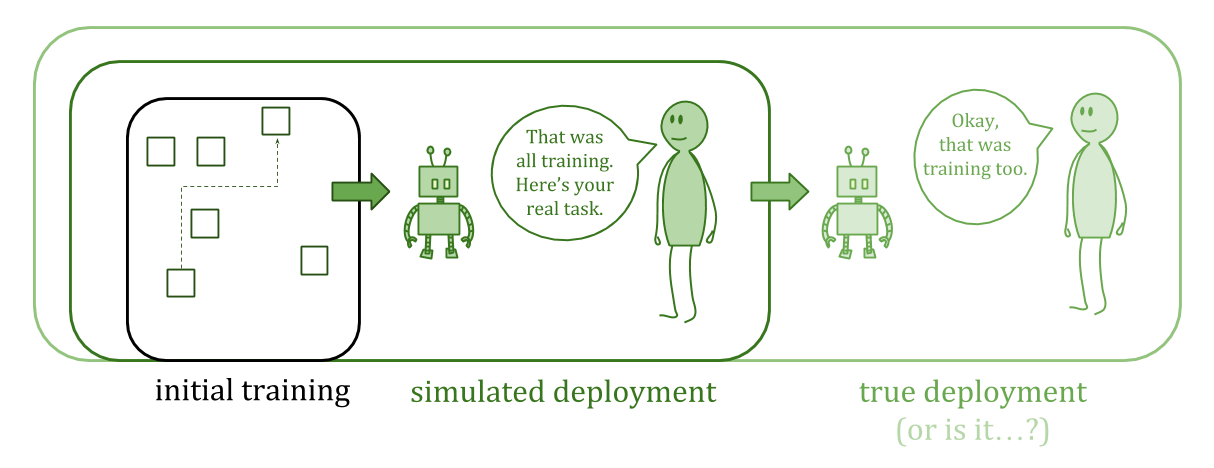
Unfortunately, convergence for this kind of learning is going to be poor. Ordinarily in machine learning, good performance means good average-case performance. But a treacherous turn is an “error” which can be carefully placed to do the most damage. We want to ensure this doesn’t happen.
The problem is, in part, that some outputs are much more important than others. Deployment is more important than training, and certain critical or vulnerable moments during deployment will be especially important. We want to be particularly sure to get important things right, rather than just getting low average loss.
But we can’t solve this by telling the system what’s important. Indeed, it seems we hope it can’t figure that out—we are banking on being able to generalize from performance on less-important cases to more-important cases. This is why research into ML techniques which avoid rare catastrophes (or “traps”) is relevant to the problem of making sure mesa-optimizers are aligned with base optimizers.
It is difficult to trust arbitrary code—which is what models from rich model classes are—based only on empirical testing. Consider a highly simplified problem: we want to find a program which only ever outputs \(1\). \(0\) is a catastrophic failure.
If we could examine the code ourselves, this problem would be easy. But the output of machine learning is often difficult to analyze; so let’s suppose that we can’t understand code at all.
Now, in some sense, we can trust simpler functions more. A short piece of code is less likely to contain a hard-coded exception. Let’s quantify that.
Consider the set of all programs of length \(L\). Some programs \(p\) will print \(1\) for a long time, but then print \(0\). We’re trying to avoid that.
Call the time-to-first-zero \(W_{p}\). (\(W_{p} = \infty\) if the program \(p\) is trustworthy, i.e., if it never outputs \(0\).)
The highest finite \(W_{p}\) out of all length-\(L\) programs is a form of the Busy Beaver function, so I will refer to it as \(BB(L)\). If we wanted to be completely sure that a random program of length \(L\) were trustworthy, we would need to observe \(BB(L)\) ones from that program.
Now, a fact about the Busy Beaver function is that \(BB(n)\) grows faster than any computable function. So this kind of empirical trust-building takes uncomputably long to find the truth, in the worst case.
What about the average case?
If we suppose all the other length-\(L\) programs are easy cases, there are exponentially many length-\(L\) programs, so the average is \(BB(L)\ / \ \mathrm{exp}(L)\). But exponentials are computable. So \(BB(L)\ / \ \mathrm{exp}(L)\) still grows faster than any computable function.
So while using short programs gives us some confidence in theory, the difficulty of forming generalized conclusions about behavior grows extremely quickly as a function of length.
If length restrictions aren’t so practical, perhaps restricting computational complexity can help us? Intuitively, a mesa-optimizer needs time to think in order to successfully execute a treacherous turn. So a program which arrives at conclusions more quickly might be more trustworthy.
However, restricting complexity class unfortunately doesn’t get around Busy-Beaver-type behavior. Strategies that wait a long time before outputting \(0\) can be slowed down even further with only slightly longer program length \(L\).
If all of these problems seem too hypothetical, consider the evolution of life on Earth. Evolution can be thought of as a reproductive fitness maximizer.
(Evolution can actually be thought of as an optimizer for many things, or as no optimizer at all, but that doesn’t matter. The point is that if an agent wanted to maximize reproductive fitness, it might use a system that looked like evolution.)
Intelligent organisms are mesa-optimizers of evolution. Although the drives of intelligent organisms are certainly correlated with reproductive fitness, organisms want all sorts of things. There are even mesa-optimizers who have come to understand evolution, and even to manipulate it at times. Powerful and misaligned mesa-optimizers appear to be a real possibility, then, at least with enough processing power.
Problems seem to arise because you try to solve a problem which you don’t yet know how to solve by searching over a large space and hoping “someone” can solve it.
If the source of the issue is the solution of problems by massive search, perhaps we should look for different ways to solve problems. Perhaps we should solve problems by figuring things out. But how do you solve problems which you don’t yet know how to solve other than by trying things?
Let’s take a step back.
Embedded world-models is about how to think at all, as an embedded agent; decision theory is about how to act. Robust delegation is about building trustworthy successors and helpers. Subsystem alignment is about building one agent out of trustworthy parts.
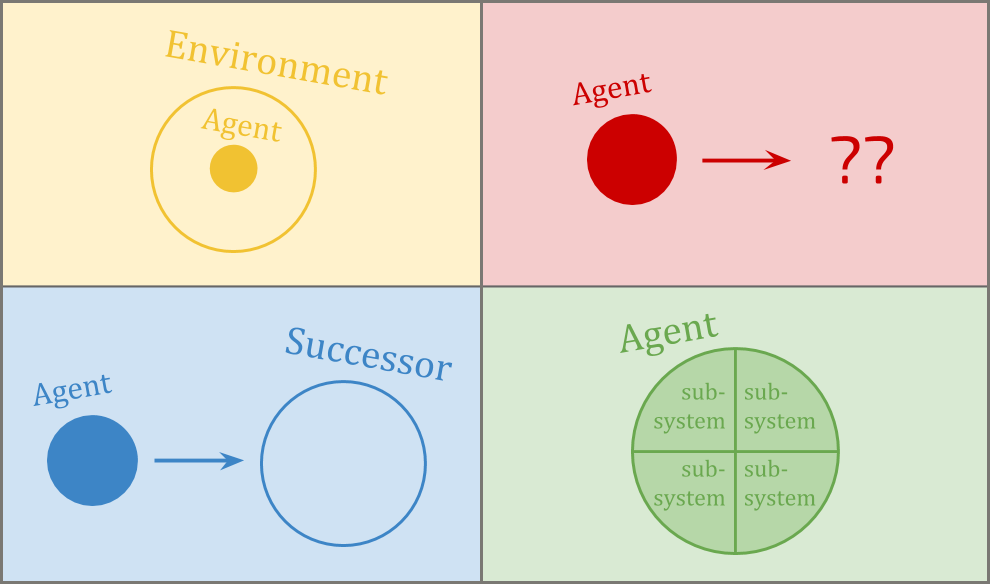
The problem is that:
- We don’t know how to think about environments when we’re smaller.
- To the extent we can do that, we don’t know how to think about consequences of actions in those environments.
- Even when we can do that, we don’t know how to think about what we want.
- Even when we have none of these problems, we don’t know how to reliably output actions which get us what we want!
This is the penultimate post in Scott Garrabrant and Abram Demski’s Embedded Agency sequence. Conclusion: embedded curiosities.
Did you like this post? You may enjoy our other Analysis posts, including: