[mathjax]
Decision theory and artificial intelligence typically try to compute something resembling
$$\underset{a \ \in \ Actions}{\mathrm{argmax}} \ \ f(a).$$
I.e., maximize some function of the action. This tends to assume that we can detangle things enough to see outcomes as a function of actions.
For example, AIXI represents the agent and the environment as separate units which interact over time through clearly defined i/o channels, so that it can then choose actions maximizing reward.
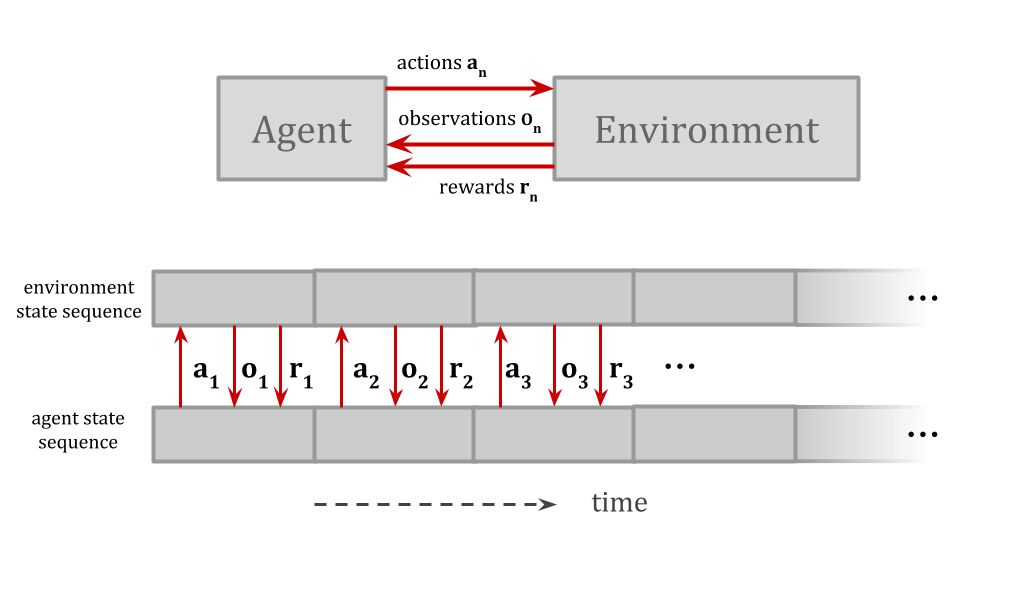
When the agent model is a part of the environment model, it can be significantly less clear how to consider taking alternative actions.
For example, because the agent is smaller than the environment, there can be other copies of the agent, or things very similar to the agent. This leads to contentious decision-theory problems such as the Twin Prisoner’s Dilemma and Newcomb’s problem.
If Emmy Model 1 and Emmy Model 2 have had the same experiences and are running the same source code, should Emmy Model 1 act like her decisions are steering both robots at once? Depending on how you draw the boundary around “yourself”, you might think you control the action of both copies, or only your own.
This is an instance of the problem of counterfactual reasoning: how do we evaluate hypotheticals like “What if the sun suddenly went out”?
Problems of adapting decision theory to embedded agents include:
- counterfactuals
- Newcomblike reasoning, in which the agent interacts with copies of itself
- reasoning about other agents more broadly
- extortion problems
- coordination problems
- logical counterfactuals
- logical updatelessness
The most central example of why agents need to think about counterfactuals comes from counterfactuals about their own actions.
The difficulty with action counterfactuals can be illustrated by the five-and-ten problem. Suppose we have the option of taking a five dollar bill or a ten dollar bill, and all we care about in the situation is how much money we get. Obviously, we should take the $10.
However, it is not so easy as it seems to reliably take the $10.
If you reason about yourself as just another part of the environment, then you can know your own behavior. If you can know your own behavior, then it becomes difficult to reason about what would happen if you behaved differently.
This throws a monkey wrench into many common reasoning methods. How do we formalize the idea “Taking the $10 would lead to good consequences, while taking the $5 would lead to bad consequences,” when sufficiently rich self-knowledge would reveal one of those scenarios as inconsistent?
And if we can’t formalize any idea like that, how do real-world agents figure out to take the $10 anyway?
If we try to calculate the expected utility of our actions by Bayesian conditioning, as is common, knowing our own behavior leads to a divide-by-zero error when we try to calculate the expected utility of actions we know we don’t take: \(\lnot A\) implies \(P(A)=0\), which implies \(P(B \& A)=0\), which implies
$$P(B|A) = \frac{P(B \& A)}{P(A)} = \frac{0}{0}.$$
Because the agent doesn’t know how to separate itself from the environment, it gets gnashing internal gears when it tries to imagine taking different actions.
But the biggest complication comes from Löb’s Theorem, which can make otherwise reasonable-looking agents take the $5 because “If I take the $10, I get $0”! And in a stable way—the problem can’t be solved by the agent learning or thinking about the problem more.
This might be hard to believe; so let’s look at a detailed example. The phenomenon can be illustrated by the behavior of simple logic-based agents reasoning about the five-and-ten problem.
Consider this example:

We have the source code for an agent and the universe. They can refer to each other through the use of quining. The universe is simple; the universe just outputs whatever the agent outputs.
The agent spends a long time searching for proofs about what happens if it takes various actions. If for some \(x\) and \(y\) equal to \(0\), \(5\), or \(10\), it finds a proof that taking the \(5\) leads to \(x\) utility, that taking the \(10\) leads to \(y\) utility, and that \(x>y\), it will naturally take the \(5\). We expect that it won’t find such a proof, and will instead pick the default action of taking the \(10\).
It seems easy when you just imagine an agent trying to reason about the universe. Yet it turns out that if the amount of time spent searching for proofs is enough, the agent will always choose \(5\)!
The proof that this is so is by Löb’s theorem. Löb’s theorem says that, for any proposition \(P\), if you can prove that a proof of \(P\) would imply the truth of \(P\), then you can prove \(P\). In symbols, with
“\(□X\)” meaning “\(X\) is provable”:
$$□(□P \to P) \to □P.$$
In the version of the five-and-ten problem I gave, “\(P\)” is the proposition “if the agent outputs \(5\) the universe outputs \(5\), and if the agent outputs \(10\) the universe outputs \(0\)”.
Supposing it is provable, the agent will eventually find the proof, and return \(5\) in fact. This makes the sentence true, since the agent outputs \(5\) and the universe outputs \(5\), and since it’s false that the agent outputs \(10\). This is because false propositions like “the agent outputs \(10\)” imply everything, including the universe outputting \(5\).
The agent can (given enough time) prove all of this, in which case the agent in fact proves the proposition “if the agent outputs \(5\) the universe outputs \(5\), and if the agent outputs \(10\) the universe outputs \(0\)”. And as a result, the agent takes the $5.
We call this a “spurious proof”: the agent takes the $5 because it can prove that if it takes the $10 it has low value, because it takes the $5. It sounds circular, but sadly, is logically correct. More generally, when working in less proof-based settings, we refer to this as a problem of spurious counterfactuals.
The general pattern is: counterfactuals may spuriously mark an action as not being very good. This makes the AI not take the action. Depending on how the counterfactuals work, this may remove any feedback which would “correct” the problematic counterfactual; or, as we saw with proof-based reasoning, it may actively help the spurious counterfactual be “true”.
Note that because the proof-based examples are of significant interest to us, “counterfactuals” actually have to be counterlogicals; we sometimes need to reason about logically impossible “possibilities”. This rules out most existing accounts of counterfactual reasoning.
You may have noticed that I slightly cheated. The only thing that broke the symmetry and caused the agent to take the $5 was the fact that “\(5\)” was the action that was taken when a proof was found, and “\(10\)” was the default. We could instead consider an agent that looks for any proof at all about what actions lead to what utilities, and then takes the action that is better. This way, which action is taken is dependent on what order we search for proofs.
Let’s assume we search for short proofs first. In this case, we will take the $10, since it is very easy to show that \(A()=5\) leads to \(U()=5\) and \(A()=10\) leads to \(U()=10\).
The problem is that spurious proofs can be short too, and don’t get much longer when the universe gets harder to predict. If we replace the universe with one that is provably functionally the same, but is harder to predict, the shortest proof will short-circuit the complicated universe and be spurious.
People often try to solve the problem of counterfactuals by suggesting that there will always be some uncertainty. An AI may know its source code perfectly, but it can’t perfectly know the hardware it is running on.
Does adding a little uncertainty solve the problem? Often not:
- The proof of the spurious counterfactual often still goes through; if you think you are in a five-and-ten problem with a 95% certainty, you can have the usual problem within that 95%.
- Adding uncertainty to make counterfactuals well-defined doesn’t get you any guarantee that the counterfactuals will be reasonable. Hardware failures aren’t often what you want to expect when considering alternate actions.
Consider this scenario: You are confident that you almost always take the left path. However, it is possible (though unlikely) for a cosmic ray to damage your circuits, in which case you could go right—but you would then be insane, which would have many other bad consequences.
If this reasoning in itself is why you always go left, you’ve gone wrong.
Simply ensuring that the agent has some uncertainty about its actions doesn’t ensure that the agent will have remotely reasonable counterfactual expectations. However, one thing we can try instead is to ensure the agent actually takes each action with some probability. This strategy is called ε-exploration.
ε-exploration ensures that if an agent plays similar games on enough occasions, it can eventually learn realistic counterfactuals (modulo a concern of realizability which we will get to later).
ε-exploration only works if it ensures that the agent itself can’t predict whether it is about to ε-explore. In fact, a good way to implement ε-exploration is via the rule “if the agent is too sure about its action, it takes a different one”.
From a logical perspective, the unpredictability of ε-exploration is what prevents the problems we’ve been discussing. From a learning-theoretic perspective, if the agent could know it wasn’t about to explore, then it could treat that as a different case—failing to generalize lessons from its exploration. This gets us back to a situation where we have no guarantee that the agent will learn better counterfactuals. Exploration may be the only source of data for some actions, so we need to force the agent to take that data into account, or it may not learn.
However, even ε-exploration doesn’t seem to get things exactly right. Observing the result of ε-exploration shows you what happens if you take an action unpredictably; the consequences of taking that action as part of business-as-usual may be different.
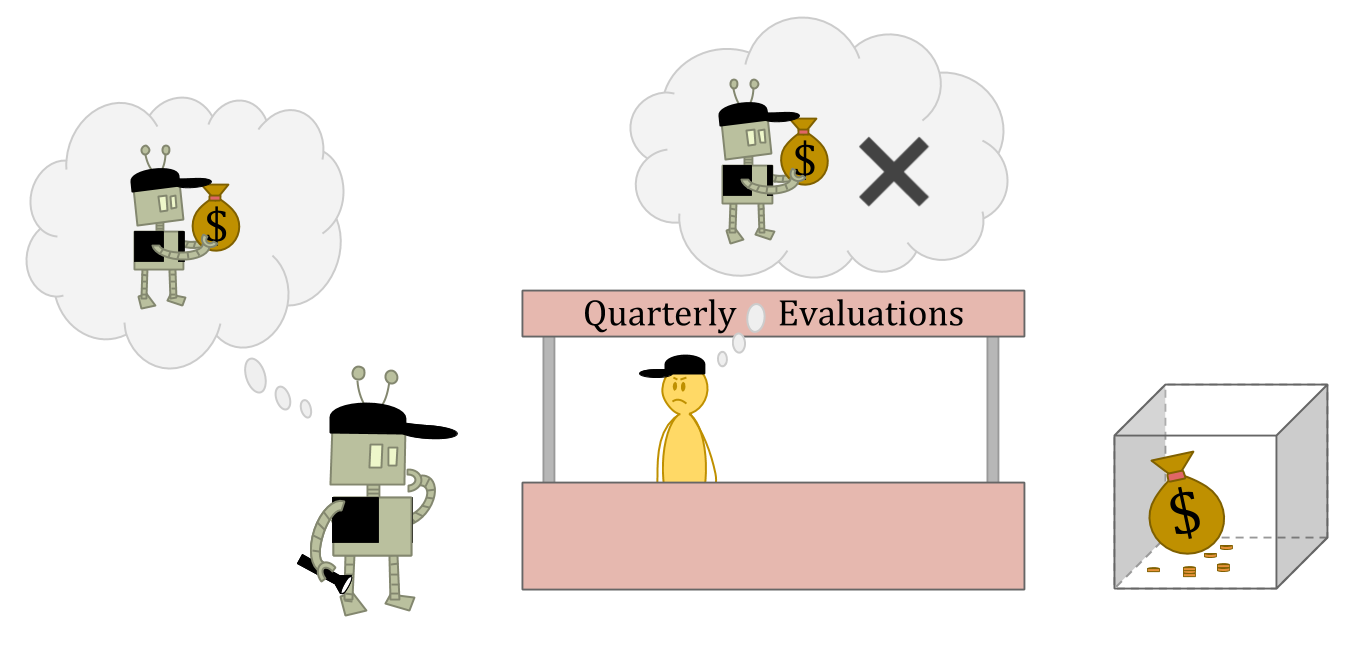
Suppose you’re an ε-explorer who lives in a world of ε-explorers. You’re applying for a job as a security guard, and you need to convince the interviewer that you’re not the kind of person who would run off with the stuff you’re guarding. They want to hire someone who has too much integrity to lie and steal, even if the person thought they could get away with it.
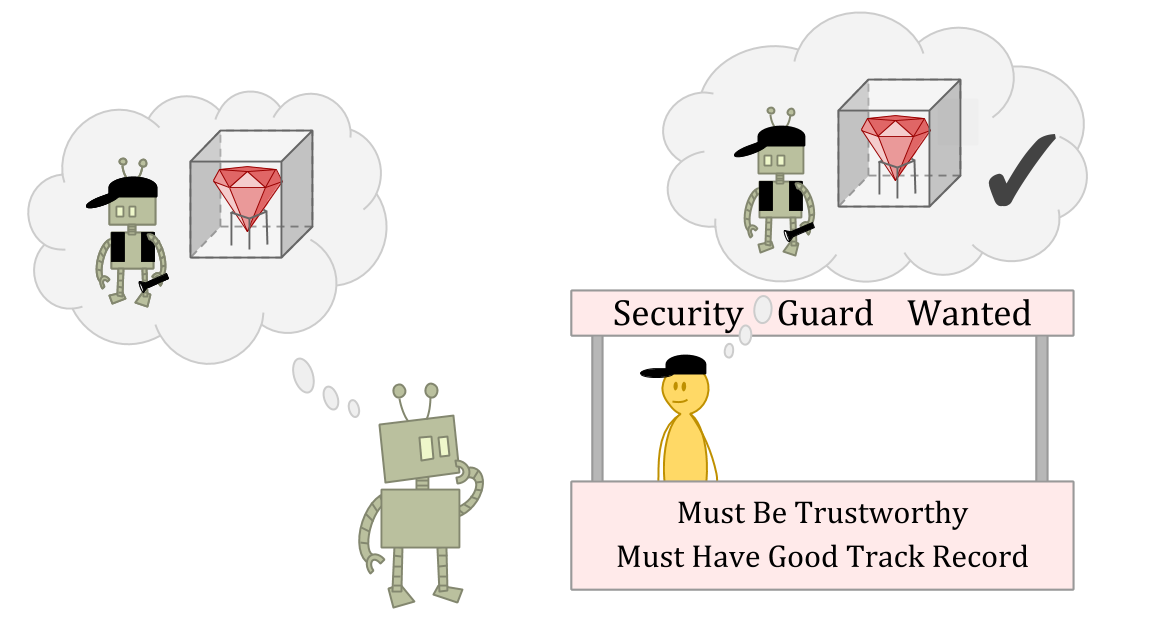
Suppose the interviewer is an amazing judge of character—or just has read access to your source code.
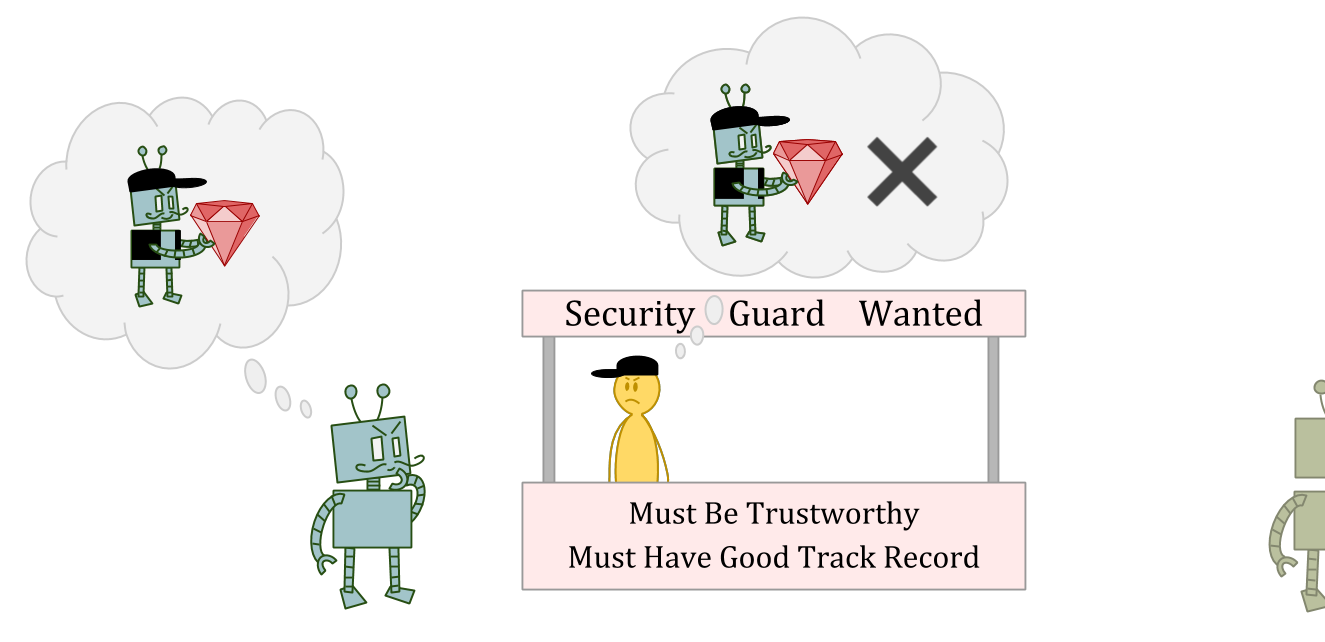
In this situation, stealing might be a great option as an ε-exploration action, because the interviewer may not be able to predict your theft, or may not think punishment makes sense for a one-off anomaly.
But stealing is clearly a bad idea as a normal action, because you’ll be seen as much less reliable and trustworthy.
If we don’t learn counterfactuals from ε-exploration, then, it seems we have no guarantee of learning realistic counterfactuals at all. But if we do learn from ε-exploration, it appears we still get things wrong in some cases.
Switching to a probabilistic setting doesn’t cause the agent to reliably make “reasonable” choices, and neither does forced exploration.
But writing down examples of “correct” counterfactual reasoning doesn’t seem hard from the outside!
Maybe that’s because from “outside” we always have a dualistic perspective. We are in fact sitting outside of the problem, and we’ve defined it as a function of an agent.

However, an agent can’t solve the problem in the same way from inside. From its perspective, its functional relationship with the environment isn’t an observable fact. This is why counterfactuals are called “counterfactuals”, after all.

When I told you about the 5 and 10 problem, I first told you about the problem, and then gave you an agent. When one agent doesn’t work well, we could consider a different agent.
Finding a way to succeed at a decision problem involves finding an agent that when plugged into the problem takes the right action. The fact that we can even consider putting in different agents means that we have already carved the universe into an “agent” part, plus the rest of the universe with a hole for the agent—which is most of the work!
Are we just fooling ourselves due to the way we set up decision problems, then? Are there no “correct” counterfactuals?
Well, maybe we are fooling ourselves. But there is still something we are confused about! “Counterfactuals are subjective, invented by the agent” doesn’t dissolve the mystery. There is something intelligent agents do, in the real world, to make decisions.
So I’m not talking about agents who know their own actions because I think there’s going to be a big problem with intelligent machines inferring their own actions in the future. Rather, the possibility of knowing your own actions illustrates something confusing about determining the consequences of your actions—a confusion which shows up even in the very simple case where everything about the world is known and you just need to choose the larger pile of money.
For all that, humans don’t seem to run into any trouble taking the $10.
Can we take any inspiration from how humans make decisions?
Well, suppose you’re actually asked to choose between $10 and $5. You know that you’ll take the $10. How do you reason about what would happen if you took the $5 instead?
It seems easy if you can separate yourself from the world, so that you only think of external consequences (getting $5).

If you think about yourself as well, the counterfactual starts seeming a bit more strange or contradictory. Maybe you have some absurd prediction about what the world would be like if you took the $5—like, “I’d have to be blind!”
That’s alright, though. In the end you still see that taking the $5 would lead to bad consequences, and you still take the $10, so you’re doing fine.

The challenge for formal agents is that an agent can be in a similar position, except it is taking the $5, knows it is taking the $5, and can’t figure out that it should be taking the $10 instead, because of the absurd predictions it makes about what happens when it takes the $10.
It seems hard for a human to end up in a situation like that; yet when we try to write down a formal reasoner, we keep running into this kind of problem. So it indeed seems like human decision-making is doing something here that we don’t yet understand.
If you’re an embedded agent, then you should be able to think about yourself, just like you think about other objects in the environment. And other reasoners in your environment should be able to think about you too.

In the five-and-ten problem, we saw how messy things can get when an agent knows its own action before it acts. But this is hard to avoid for an embedded agent.
It’s especially hard not to know your own action in standard Bayesian settings, which assume logical omniscience. A probability distribution assigns probability 1 to any fact which is logically true. So if a Bayesian agent knows its own source code, then it should know its own action.
However, realistic agents who are not logically omniscient may run into the same problem. Logical omniscience forces the issue, but rejecting logical omniscience doesn’t eliminate the issue.
ε-exploration does seem to solve that problem in many cases, by ensuring that agents have uncertainty about their choices and that the things they expect are based on experience.

However, as we saw in the security guard example, even ε-exploration seems to steer us wrong when the results of exploring randomly differ from the results of acting reliably.
Examples which go wrong in this way seem to involve another part of the environment that behaves like you—such as another agent very similar to yourself, or a sufficiently good model or simulation of you. These are called Newcomblike problems; an example is the Twin Prisoner’s Dilemma mentioned above.

If the five-and-ten problem is about cutting a you-shaped piece out of the world so that the world can be treated as a function of your action, Newcomblike problems are about what to do when there are several approximately you-shaped pieces in the world.
One idea is that exact copies should be treated as 100% under your “logical control”. For approximate models of you, or merely similar agents, control should drop off sharply as logical correlation decreases. But how does this work?

Newcomblike problems are difficult for almost the same reason as the self-reference issues discussed so far: prediction. With strategies such as ε-exploration, we tried to limit the self-knowledge of the agent in an attempt to avoid trouble. But the presence of powerful predictors in the environment reintroduces the trouble. By choosing what information to share, predictors can manipulate the agent and choose their actions for them.
If there is something which can predict you, it might tell you its prediction, or related information, in which case it matters what you do in response to various things you could find out.
Suppose you decide to do the opposite of whatever you’re told. Then it isn’t possible for the scenario to be set up in the first place. Either the predictor isn’t accurate after all, or alternatively, the predictor doesn’t share their prediction with you.
On the other hand, suppose there’s some situation where you do act as predicted. Then the predictor can control how you’ll behave, by controlling what prediction they tell you.
So, on the one hand, a powerful predictor can control you by selecting between the consistent possibilities. On the other hand, you are the one who chooses your pattern of responses in the first place. This means that you can set them up to your best advantage.
So far, we’ve been discussing action counterfactuals—how to anticipate consequences of different actions. This discussion of controlling your responses introduces the observation counterfactual—imagining what the world would be like if different facts had been observed.
Even if there is no one telling you a prediction about your future behavior, observation counterfactuals can still play a role in making the right decision. Consider the following game:
Alice receives a card at random which is either High or Low. She may reveal the card if she wishes. Bob then gives his probability \(p\) that Alice has a high card. Alice always loses \(p^2\) dollars. Bob loses \(p^2\) if the card is low, and \((1-p)^2\) if the card is high.
Bob has a proper scoring rule, so does best by giving his true belief. Alice just wants Bob’s belief to be as much toward “low” as possible.
Suppose Alice will play only this one time. She sees a low card. Bob is good at reasoning about Alice, but is in the next room and so can’t read any tells. Should Alice reveal her card?
Since Alice’s card is low, if she shows it to Bob, she will lose no money, which is the best possible outcome. However, this means that in the counterfactual world where Alice sees a high card, she wouldn’t be able to keep the secret—she might as well show her card in that case too, since her reluctance to show it would be as reliable a sign of “high”.
On the other hand, if Alice doesn’t show her card, she loses 25¢—but then she can use the same strategy in the other world, rather than losing $1. So, before playing the game, Alice would want to visibly commit to not reveal; this makes expected loss 25¢, whereas the other strategy has expected loss 50¢. By taking observation counterfactuals into account, Alice is able to keep secrets—without them, Bob could perfectly infer her card from her actions.
This game is equivalent to the decision problem called counterfactual mugging.
Updateless decision theory (UDT) is a proposed decision theory which can keep secrets in the high/low card game. UDT does this by recommending that the agent do whatever would have seemed wisest before—whatever your earlier self would have committed to do.
As it happens, UDT also performs well in Newcomblike problems.
Could something like UDT be related to what humans are doing, if only implicitly, to get good results on decision problems? Or, if it’s not, could it still be a good model for thinking about decision-making?
Unfortunately, there are still some pretty deep difficulties here. UDT is an elegant solution to a fairly broad class of decision problems, but it only makes sense if the earlier self can foresee all possible situations.
This works fine in a Bayesian setting where the prior already contains all possibilities within itself. However, there may be no way to do this in a realistic embedded setting. An agent has to be able to think of new possibilities—meaning that its earlier self doesn’t know enough to make all the decisions.
And with that, we find ourselves squarely facing the problem of embedded world-models.
This is part of Abram Demski and Scott Garrabrant’s Embedded Agency sequence. Continued here!